Kezdőlap


Feladat:	1956. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1956/november, 75 - 77. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Érintőnégyszögek, Pitagorasz-tétel alkalmazásai, Derékszögű háromszögek geometriája, Beírt kör, Hozzáírt körök, Háromszögek hasonlósága, Arany Dániel
Hivatkozás(ok):	Feladatok: 1956/szeptember: 1956. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük az $A B$ és $C D$ oldalak hosszát $a$ -val és $c$ -vel, az $A B$ , $B C$ , $C D$ , $D A$ oldalakon levő érintési pontokat $P$ , $Q$ , $R$ , $S$ -sel. Bocsássunk merőlegest a $C$ és $D$ pontokból az $A B$ egyenesre (1. ábra).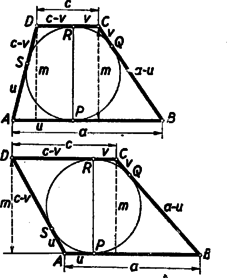

1. ábra

Két derékszögű háromszög keletkezik, melyek átfogója a

B C

, ill.

D A

oldal, egyik befogója a trapéz

m

magasságával, másik pedig a

B P

és

C R

, illetőleg a

D R

és

A P

érintőszakaszok különbségének abszolút értékével egyenlő. Mivel a körhöz egy pontból húzott érintőszakaszok egyenlők, így

\begin{matrix} B P = B Q = a - u, D R = D S = c - v, \end{matrix}

tehát a derékszögű háromszögekre Pythagoras tételét alkalmazva

\begin{matrix} {(a - u + v)}^{2} = m^{2} + | a - u - v |^{2}, \\ {(u + c - v)}^{2} = m^{2} + | u - (c - v) |^{2} . \end{matrix}

Miután egy számnak és negatívjának a négyzete megegyezik, az abszolútérték-jeleket elhagyhatjuk. A második egyenletet az elsőből levonva az

\begin{matrix} {[a - (u - v)]}^{2} - {[c + (u - v)]}^{2} = {[a - (u + v)]}^{2} - {[(u + v) - c]}^{2} \end{matrix}

összefüggéshez jutunk. Ebből a zárójelek felbontása és rendezés után kapjuk, hogy

\begin{matrix} 4 a v = 4 c u, \end{matrix}

ami egyenértékű a bizonyítandó összefüggéssel.

II. megoldás: A beírt kör

O

középpontja a trapéz szögfelezőinek metszéspontja. Mivel a trapéz

B

-nél és

C

-nél levő szögeinek összege

180^{\circ}

, azért a

B O C

háromszög

B

-nél és

C

-nél levő szögeinek összege

90^{\circ}

, és így a háromszög

O

-nál derékszögű (2. ábra).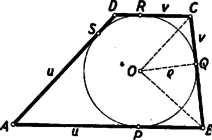

2. ábra

Az átfogóra bocsátott magasság a beírt kör sugara,

ϱ

. Így a derékszögű háromszögre vonatkozó középarányossági tételek szerint

\begin{matrix} ϱ^{2} = B Q \cdot C Q . \end{matrix}

Hasonlóan adódik a

D O A

háromszögből, hogy

\begin{matrix} ϱ^{2} = D S \cdot A S, \end{matrix}

tehát a jobb oldalak is egyenlők. Felhasználva ezt és azt, hogy körhöz egy pontból húzott érintőszakaszok egyenlők, nyerjük, hogy

\begin{matrix} u \cdot C D = A S (D R + R C) = A S (D S + v) = A S \cdot D S + A S \cdot v = B Q \cdot C Q + \\ + A S \cdot v = B P \cdot v + A P \cdot v = A B \cdot v, \end{matrix}

és ezt kellett bizonyítanunk.

III. megoldás: Az állítás nyilvánvaló, ha

B C ∥ D A

, ezért feltehetjük, hogy a

B C

és

D A

oldalaknak mondjuk a

C

-n és

D

-n túli meghosszabbításai metszik egymást egy

E

pontban. Érintse a trapézba írt kör a párhuzamos oldalakat a

P

és

R

pontban, a

C D E

háromszögbe írt kör pedig a

C D

oldalt az

R'

pontban (3. ábra).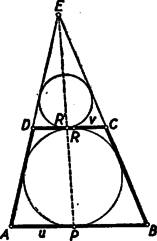

3. ábra

A trapézba írt kör a

C D E

háromszögnek hozzáírt köre, és egyben az

A B E

háromszögnek beírt köre. Ismeretes, a hozzáírt és beírt körre nézve a

\begin{matrix} C R = D R' \end{matrix}

összefüggés.
Mivel az

A B E

és

D C E

háromszögek hasonlók és

R'

és

P

e hasonlóságnál egymásnak megfelelő pontok, így fennáll az

\begin{matrix} \frac{A B}{C D} = \frac{A P}{D R'} = \frac{A P}{C R} = \frac{u}{v} \end{matrix}

összefüggés, ami a bizonyítandó állításnak csak átrendezett alakja.

Megjegyzések. Sokan abból kiindulva bizonyították a tételt, hogy a párhuzamos oldalak érintési pontjait összekötő egyenes átmegy az átlók metszéspontján, vagy, hogy érintőnégyszögben az átlók és a szemközti oldalakon levő érintési pontokat összekötő egyenesek egy ponton mennek keresztül. Ez az állítás ugyan igaz, de bizonyítása sokkal nehezebb, mint a feladat állításáé. Mások viszont abból a hamis állításból indultak ki, mely szerint két négyszög hasonló volna, ha megfelelő szögeik egyenlők.