Kezdőlap


Feladat:	1956. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1956/október, 33 - 35. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Egyenlő szárú háromszögek geometriája, Háromszög-egyenlőtlenség alkalmazásai, Arany Dániel
Hivatkozás(ok):	Feladatok: 1956/szeptember: 1956. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az adott szögkülönbséget $δ$ -val. Ha a $c$ oldal és a kerület adott, akkor ismert a másik két oldal összege $a + b$ is. A szerkeszthetőséghez természetesen szükséges, hogy

\begin{matrix} a + b = k - c > c, \end{matrix}

azaz

\begin{matrix} 2 c < k \end{matrix}

legyen.
Forgassuk rá egy tetszésszerinti

A B C

háromszögben pl. a

B C = a

oldal meghosszabbítására a

C A' = b

oldalt (1. ábra).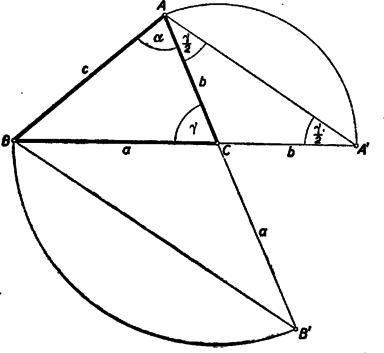

1. ábra

A keletkezett

A C A'

egyenlő szárú háromszög

C

csúcsánál levő külső szöge az

A B C

háromszög

γ

szöge, így az

A A'

alapon fekvő szögek

\frac{γ}{2}

nagyságúak.
Számítsuk ki a keletkező

A B A'

háromszögben az

A

-nál levő szöget:

\begin{matrix} A' A B ∢ = α + \frac{γ}{2} = α + \frac{180^{\circ} - (α + β)}{2} = 90^{\circ} + \frac{α - β}{2} = 90^{\circ} + \frac{δ}{2} . \end{matrix}

A A' B

háromszögben ismert tehát két oldal és a nagyobbikkal szemközti szög, így ez egyértelműen megszerkeszthető. Az

A A'

oldal felező merőlegese metszi ki az

A' B

oldalból a

C

pontot (2. ábra).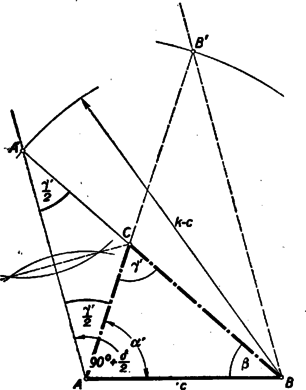

2. ábra

Ez a

B A'

oldal belsejére esik, mert az

A' A B

szög tompaszög.
A keletkezett

A B C

háromszög kielégíti a feltételeket, mert ‐ szögeit

α'

β'

γ'

-vel jelölve ‐ az

A C A'

háromszög szerkesztés szerint egyenlő szárú, így az alapon fekvő szögei feleakkorák, mint a

C

csúcsnál levő külső szög,

γ'

. Ezért

\begin{matrix} α' - β' = 90^{\circ} + \frac{δ}{2} - \frac{γ'}{2} - β' = 90^{\circ} + \frac{δ}{2} - \frac{180^{\circ} - (α' + β')}{2} - β' = \frac{δ}{2} + \frac{α' - β'}{2} . \end{matrix}

Innen

\begin{matrix} α' - β' = δ, \end{matrix}

másrészt a

C

csúcsból induló oldalak összege

\begin{matrix} A C + C B = A' C + C B = A' B, \end{matrix}

szintén az előírt

k - c

érték.

Megjegyzés: Az

A A'

oldal a

C

csúcsból induló szögfelezővel párhuzamos, és ha az

A C

oldal meghosszabbítására mérjük rá a

C B

-vel egyenlő

C B'

távolságot, akkor ugyanúgy

B B'

is párhuzamos a szögfelezővel. (1. ábra). A szerkesztés ennek alapján úgy is befejezhető, hogy az

A A' B

háromszög után ugyanarra az

A B

oldalra megszerkesztjük az

A B B'

háromszöget

(B B' | | A A'

és

A B' = k - c)

is. Ekkor

C

A B'

és

A' B

oldalak metszéspontjaként adódik (2. ábra).