Kezdőlap


Feladat:	1955. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1955/november, 81 - 84. oldal		PDF \| MathML
Témakör(ök):	Háromszögek szerkesztése, Szögfelező egyenes, Háromszögek hasonlósága, Trapézok, Négyszögek középvonalai, Arany Dániel
Hivatkozás(ok):	Feladatok: 1955/szeptember: 1955. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: A feladatot megoldhatjuk számítás segítségével. Jelöljük az érintőkörök középpontját $O_{b}$ és $O_{c}$ -vel, érintési pontjukat a $B C$ egyenesen $T_{b}$ és $T_{c}$ -vel (5. 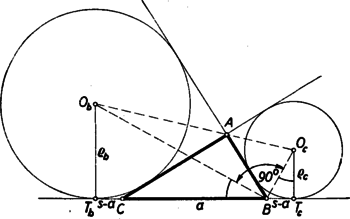ábra).

5. ábra

Ismeretes, hogy

B T_{b} = C T_{c} = s

, ahol

s

a háromszög kerületének felét jelenti.

B

-t összekötve a körközéppontokkal tudjuk, hogy

B O_{b}

és

B O_{c}

a háromszög

B

-nél levő belső és külső szögfelezői, és így egymásra merőlegesek.
Ebből következik, hogy

\begin{matrix} B O_{c} T_{c} ∢ = O_{b} B T_{b} ∢, \end{matrix}

mint merőlegesszárú szögek egyenlők, következőleg

B O_{c} T_{c}

és

O_{b} B T_{b}

háromszögek hasonlók. A befogók arányát felírva

\begin{matrix} \frac{O_{c} T_{c}}{T_{c} B} = \frac{B T_{b}}{T_{b} O}, azaz \frac{ϱ_{c}}{s - a} = \frac{s}{ϱ_{b}}, s^{2} - a s - ϱ_{b} ϱ_{c} = 0. \end{matrix}

Innen

s

-et kiszámítva (a pozitív gyököt véve)

\begin{matrix} s = \frac{a}{2} + \sqrt[]{{(\frac{a}{2})}^{2} + ϱ_{b} ϱ_{c}} . \end{matrix}

Ez a távolság megszerkeszthető; a második tag pl. a következő módon: mérjük fel egy egyenesre közös

P

pontból ellenkező irányban a

P Q = ϱ_{b}, P R = ϱ_{c}

távolságot (6. ábra).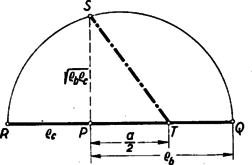

6. ábra

Az egyenesre

P

-ben emelt merőleges messe a

Q R

, mint átmérő fölé emelt félkört

S

-ben akkor ‐ mint ismeretes ‐

P S = \sqrt[]{ϱ_{b} ϱ_{c}}

P

-ből felmérve a

Q R

egyenesre (bármelyik irányban) a

P T = \frac{a}{2}

távolságot

\begin{matrix} S T = \sqrt[]{P T^{2} + P S^{2}} = \sqrt[]{{(\frac{a}{2})}^{2} + ϱ_{b} ϱ_{c}} \end{matrix}

s = B T_{b} = C T_{c}

, alapján a

B C

egyenesen megszerkeszthetjük a

T_{b}

és

T_{c}

, pontokat. A többi már triviális.

II. megoldás: Az előző megoldás jelöléseit használva, ott azt láttuk be, hogy az

O_{b} O_{c}

szakasz a

B

pontból ‐ és természetesen ugyanúgy a

C

pontból is ‐ derékszögben látszik. Ezt az előbbinél sokkal egyszerűbben is felhasználhatjuk a háromszög megszerkesztésére. A nyert összefüggés szerint az

O_{b} O_{c}

, mint átmérő fölé emelt félkör átmegy

B

-n és

C

-n (7. ábra).

7. ábra

A kör

K

középpontjából a

B C

egyenesre bocsátott merőleges egyrészt felezi a

B C

szakaszt, mint a kör húrját, másrészt hossza, mint az

O_{b} T_{b} T_{c} O_{c}

trapéz középvonala

\frac{ϱ_{b} + ϱ_{c}}{2}

hosszúságú.
Ennek alapján a szerkesztés a következőképpen történhetik: Egy

a

hosszúságú

B C

szakasz

D

felezőpontjában

D K = \frac{ϱ_{b} + ϱ_{c}}{2}

hosszúságú merőlegest emelünk (8. ábra).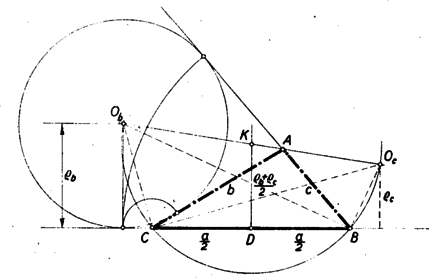

8. ábra

Megrajzoljuk a

K

középpontú

B

-n és

C

-n átmenő kört és ennek a

K D

egyenestől a

C

pont felé eső félkörét elmetsszük a

B C

egyenestől

ϱ_{b}

távolságban. Az

O_{b}

pont körüli,

B C

egyenest érintő kör

B

-ből és

C

-ből húzott érintője lesz a háromszög másik két oldala.
Be kell látnunk, hogy a háromszög megfelel a feltételeknek, tehát hogy

c

oldalához hozzáírt kör

ϱ_{c}

, sugarú. Azt mutatjuk meg, hogy e hozzáírt kör középpontja a

K

középponttal rajzolt kör

O_{b}

pontjával átelenes

O_{c}

, pont és ez a

B C

egyenestől

ϱ_{c}

távolságra van. Az előbbi következik abból, hogy

O_{c}

, a háromszög

C

pontban levő belső szögének és a

B

csúcsú külszögnek a szögfelezőin van. Ennek igazolására tekintsük az

O_{b}

középpontú

ϱ_{b}

sugarú kört. Ez szerkesztés szerint hozzáírt köre a háromszögnek, tehát

O_{b} C

felezi a

C

csúcsnál levő külső szöget,

O_{b} B

pedig a

B

-nél levő belső szöget. Így a

C O_{c}

és

B O_{c}

egyenesek, amelyek az előbbiekre merőlegesek, valóban felezik a

C

-nél levő belső szöget, ill. a

B

-nél levő külső szöget. Másrészt

O_{b}

-ből és

O_{c}

-ből merőlegest bocsátva a

B C

egyenesre trapézt kapunk, amelynek

O_{b}

-ből induló párhuzamos oldala

ϱ_{b}

hosszúságú,

K

-ból induló középvonala pedig

\frac{ϱ_{b} + ϱ_{c}}{2}

hosszúságú. Így az

O_{c}

-ből induló oldal hossza valóban

ϱ_{c}

III. megoldás: Készítsünk vázlatot (7. ábra). A

C A

oldalhoz hozzáírt

ϱ_{b}

sugarú kör érintse a

B C

egyenest

D

-ben,

C A

-t

E

-ben, az

A B

oldalhoz hozzáírt

ϱ_{c}

sugarú kör

C A

-n levő érintési pontja legyen

F

; a háromszög kerületének felét jelöljük

s

-sel.
Ekkor

\begin{matrix} B D = C F = s, C D = C E = s - a, \end{matrix}

tehát

\begin{matrix} E F = C F = C E = s - (s - a) = a . \end{matrix}

Ennek alapján a következő szerkesztés nyerhető:

E F = a

hosszúságú szakaszhoz rajzoljunk ellenkező oldalról

E

-ben érintő

ϱ_{b}

sugarú és

F

-ben érintő

ϱ_{c}

sugarú kört (9. ábra).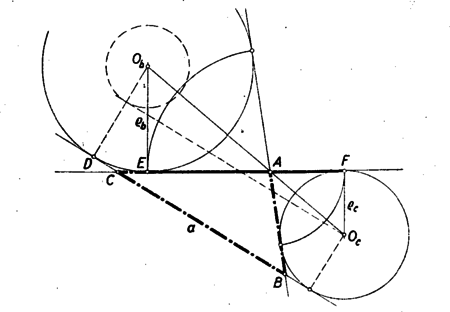

9. ábra

Szerkesszük meg a második belső közös érintőt és egy külső közös érintőt. Az érintők zárják közre a kívánt háromszöget. Jelöléseket az ábra szerint választva azt kell igazolnunk, hogy

B C = a

, ez pedig a fenti számoláshoz hasonlóan következik:

\begin{matrix} a = E F = C F - C E = s - C E = D B - D C = C B . \end{matrix}

Megjegyzés: A helyes megoldók többsége csak bonyolult számításokkal oldotta meg a feladatot.