Kezdőlap


Feladat:	1955. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1955/október, 36 - 38. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Középponti és kerületi szögek, Deltoidok, Tengelyes tükrözés, Arany Dániel
Hivatkozás(ok):	Feladatok: 1955/szeptember: 1955. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a $C$ -ből induló szögfelező és $D E$ metszéspontja $F$ , a szögfelezők metszéspontja $O$ . (2. ábra. ‐ Felhasználjuk tehát azt a tételt, amely szerint a belső szögfelezők egy pontban metszik egymást.)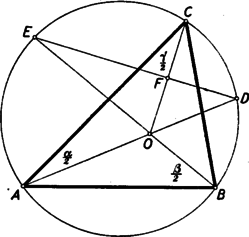

2. ábra

Ekkor, mint az

A O C_{▵}

külső szöge

\begin{matrix} C O D ∢ \equiv F O D ∢ = \frac{α}{2} + \frac{γ}{2} . \end{matrix}

A kerületi szögek tétele szerint

\begin{matrix} A D E ∢ \equiv O D F ∢ = \frac{β}{2} . \end{matrix}

Így a

D F O

háromszögből

\begin{matrix} D F O ∢ = 180^{\circ} - (O D F ∢ + F O D ∢) = 180^{\circ} - \frac{α + β + γ}{2} = 90^{\circ} . \end{matrix}

D E

tehát merőleges a

C

-ből induló szögfelezőre.

II. megoldás: A

D

ill.

E

pont felezi a körülírt körnek a

B C

, ill.

A C

oldalak fölötti ívét. Így az egyenlő íveken nyugvó kerületi szögek egyenlő volta miatt a

C D O E

négyszögben a

D E

átló felezi a végpontjainál levő szögeket (3. ábra), tehát szimmetria-tengelye a négyszögnek. (A négyszög deltoid.)

3. ábra

Mivel

C

és

O

egymás tükörképei

D E

-re nézve, azért

\begin{matrix} D E ⊥ C O, \end{matrix}

C O

C

-ből induló szögfelező, mert

O

-n kell átmennie a harmadik szögfelezőnek is.

III. megoldás: A

C D O E

négyszög deltoid voltát a következőképpen is bizonyíthatjuk:
Ha a

B

és

C

pontokat rögzítjük és

A

végigfut a

\hat{B E C}

íven, akkor

O

annak a körnek

B C

ívén fut végig, amelynek középpontja

D

(3. ábra ‐ lásd a tavaly A. D. verseny I. forduló 1. feladatát a K. M. L. 1954 októberi számában). Hasonlóképpen

A

és

C

rögzítése és a

B

pont mozgása esetén

O

mértani helye az

E

középpontú

A C

körív. Tehát

\begin{matrix} D C = D O és E C = E O, \end{matrix}

ami bizonyítandó volt.

A további megoldások nem használják fel a szögfelezők metszéspontjára vonatkozó tételt.

IV. megoldás. Jelölje

G

C

-ből húzott szögfelező metszéspontját a körrel (4. ábra).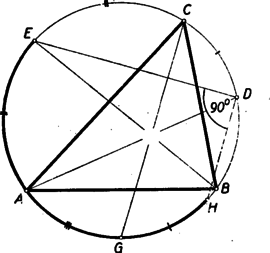

4. ábra

D

E

és

G

felezik a háromszög oldalai feletti köríveket. Húzzunk

D

-ből párhuzamost

C G

-vel. Legyen ennek második metszéspontja a körrel

H

. Ekkor

\begin{matrix} {C H}_{}^{⌢} = {C D}_{}^{⌢}, \end{matrix}

így az

\hat{E A G H}

körív a három oldal fölötti körívnek felerészeiből tevődik össze, vagyis félkör.
Ebből következik, hogy

\begin{matrix} E D H ∢ = 90^{\circ}, \end{matrix}

és így a

D H | | C G

összefüggés folytán

\begin{matrix} D E ⊥ C G . \end{matrix}

Megjegyzés: Tulajdonképpen azt az általános tételt bizonyítottuk az itt szereplő speciális esetre, hogy két húr szöge akkora, mint a szög és csúcsszögével szemközti ívek összege fölötti kerület szögek a körben. Az itt használt bizonyítás tetszés szerinti húrokra átvihető.
A feladat néhány további megoldása lényegében e tétel más segédvonalak alapján történő bizonyításaiban állt. (Ezeket itt nem közöljük.)

V. megoldás: Messe a

D E

egyenes az

A C

és

B C

oldalt K-ban és L-ben. Több versenyző azt mutatta ki, hogy a

C K L

háromszög egyenlő szárú. Ebből következik, hogy

D E

merőleges a

C

-ből induló szögfelezőre, mert egyenlőszárú háromszögben az alap és a csúcsnál levő szög szögfelezője merőlegesek egymásra.

5. ábra

Az egyenlőszárúság például így látható be egyszerűen: Mivel

E

felezi az

A C

körívet,

D

B C

körívet (5. ábra), azért

\begin{matrix} C E D ∢ = B C D ∢ és A C E ∢ = C D E ∢, \end{matrix}

mint egyenlő köríveken nyugvó kerületi szögek. Ebből következik, hogy a

C K E_{▵}

és

D L C_{▵}

harmadik szögei is egyenlők, amelyek egyben a

C K L_{▵}

háromszög

K

-nál és

L

-nél levő külső szögei.
Így a

C K L

háromszög egyenlő szárú.

VI. megoldás: Legyen

C_{0}

A B

fölötti

C

-t tartalmazó körív felezőpontja. Az

A B C_{0}

egyenlőszárú háromszőg

C_{0}

-ból induló szögfelezője az ábrának szimmetriatengelye s így az

A B C_{0}

másik két szögfelezőjének,

D_{0}

és

E_{0}

metszéspontjait összekötő egyenes merőleges rá (6. ábra).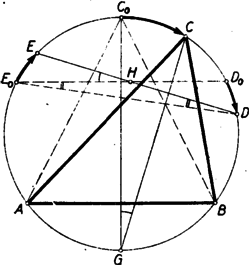

6. ábra

Ha most

C_{0}

elmozdul a kör mentén

C

-be, akkor

D_{0}

és

E_{0}

ugyanolyan irányban feleakkora körívvel mozdulnak el. Legyen

D_{0}

E_{0}

és

D E

metszéspontja

H

. A mondottak szerint

\begin{matrix} D_{0} E_{0} D ∢ = E D E_{0} ∢ = \frac{1}{2} C_{0} G C ∢ . \end{matrix}

Ennek folytán, mint az

E_{0} D H

háromszög külső szöge

\begin{matrix} E_{0} H E ∢ = H E_{0} D ∢ + H D E_{0} ∢ = C_{0} G C ∢, \end{matrix}

vagyis a

D E

egyenes ugyanakkora szöggel fordult el, mint a

C

csúcsból induló szögfelező, merőlegességük tehát megmaradt.