Feladat: 1955. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1955/november, 76 - 78. oldal  PDF  |  MathML 
Témakör(ök): Trapézok, Párhuzamos szelők tétele és megfordítása, Kör geometriája, Középponti és kerületi szögek, Thalesz-kör, Arany Dániel
Hivatkozás(ok):Feladatok: 1955/szeptember: 1955. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen AC és DP metszéspontja E, továbbá messe a PA egyenes a kör D-ben húzott érintőjét F-ben (1. ábr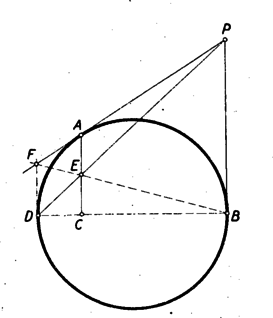a).

 
 
1. ábra
 

Bebizonyítjuk, hogy E a BPFD trapéz átlóinak metszéspontja. Egyrészt
FD=FAésPA=PB,
mint egy pontból húzott érintők. Az átlók metszéspontja az átlókat a párhuzamos oldalak arányában osztja, ugyanúgy, mint A az FP szakaszt, tehát az A-t az átlók metszéspontjával összekötő egyenes párhuzamos a párhuzamos oldalakkal s így azonos az AC egyenessel.
Ismert tétel szerint* az átlók metszéspontja felezi a rajta át a párhuzamos oldalakkal párhuzamosan húzott szakaszt, s így a feladat állítását igazoltuk.
 

II. megoldás: Messe DA meghosszabbítása BP-t Q-ban (2. ábra).
 
 
2. ábra
 

Mivel az ABP háromszög egyenlő szárú, így az ABQ derékszögű háromszögben a PAQ és PQA szögek egyenlő szögeket pótolnak 90∘-ra vagyis az APQ háromszög is egyenlő szárú. Így QP=PB, tehát DP a BDQ háromszög súlyvonala, tehát felezi a BQ-val párhuzamos AC szakaszt is, és ez volt a bizonyítandó.
III. megoldás: Az AD egyenes párhuzamos a P pontot a kör O középpontjával összekötő egyenessel (3. ábra).
 
 
3. ábra
 

Ugyanis az AB egyenes merőleges AD-re. Thales tétele szerint, PQ-ra pedig azért, mert utóbbi szögfelezője, az előbbi pedig alapja az APB egyenlőszárú háromszögnek.
Mivel O felezi a BD szakaszt, ezért P is felezi a BP egyenesnek B-től az AD egyenessel való Q metszéspontjáig terjedő szakaszát. DP tehát súlyvonala a BDQ háromszögnek s így felezi a BQ-val párhuzamos AC szakaszt is. Ezzel igazoltuk a feladat állítását.
Jegyzet: AD és PO párhuzamossága sok más úton is belátható, például így: az ADB kerületi szög fele az AOB középponti szögnek (3. ábra). Mivel a két szög B-n átmenő szárai egy egyenesbe esnek, így AD párhuzamos a középponti szög felezőjével, ez pedig a PO egyenes, mert a PAOB négyszög deltoid.
 

Megjegyzés: Itt a leggyakoribb hiba az volt (mint az a bizonyítási feladatnál általában lenni szokott), hogy a bizonyítandó tétellel egyenértékű állítást használtak fel a versenyzők bizonyítás nélkül. Pl. az 1. ábrában feltételezték, hogy BE és FE szakaszok egy egyenesen vannak stb.
*Matematika gimnáziumok II. osztálya számára. Tankönyvkiadó 1953. 30. old.