Feladat:	1954. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1954/november, 89 - 93. oldal		PDF  |  MathML
Témakör(ök):	Mozgással kapcsolatos szöveges feladatok, Másodfokú (és arra visszavezethető) egyenletrendszerek, Egyenletrendszerek grafikus megoldása, Arany Dániel
Hivatkozás(ok):	Feladatok: 1954/szeptember: 1954. évi Arany Dániel matematikaverseny 2. forduló haladók (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.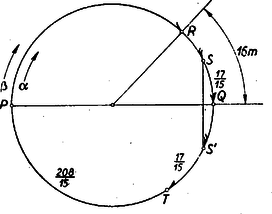     1. ábra   I. megoldás: Az 1. ábrán a kör belső oldalán $\alpha$ helyzetét, a külsőn ugyanakkor $\beta$ helyzetét tüntettük fel egyforma fél nyilakkal és köztük a megfelelő futóknak egy-egy ív befutására szükséges idejét. Válasszuk a befutási időket ismeretlennek: fussa be $\alpha$ a félkört $x$ másodperc alatt, $\beta$ pedig $y$ másodperc alatt. Mivel egyenletesen futnak, $\alpha$ bármely utat $\frac{x}{y}$-szor annyi idő alatt fut be, mint amennyi alatt $\beta$ ezt az utat befutja. Az $\widehat{SQ}$ utat $\beta$ befutotta $\frac{17}{15}$ sec alatt, $\alpha$ tehát $\frac{17}{15}\frac{x}{y}$ sec alatt futja be ezt az utat és a vele egyenlő $\widehat{QS\text{'}}$ utat is; ugyanannyi idő alatt $\beta$ viszont $R$-ből $S$-be érkezett. Nézzük meg, mennyi idő alatt tette meg $\alpha$ a $QP$ második félkört és mennyi alatt $\beta$ a $\widehat{PQ}$ első félkört. Tudjuk, hogy ezen idő éppen $x$-szel, ill. $y$-nal egyenlő. A $\widehat{QS\text{'}}$, $\widehat{S\text{'}T}$, $\widehat{TP}$ ívek befutására $\alpha$-nak szükséges időket összeadva $\begin{array}{c}{\displaystyle x=\frac{17}{15}\frac{x}{y}+\frac{17}{15}+\frac{208}{15}=\frac{17x}{15y}+15.}\end{array}$ (1) Míg $\beta$ elért $P$-ből $R$-be, addig $\alpha$ a félkört futotta be, tehát ezalatt $x$ sec telt el. Az $\widehat{RS}$ úthoz pedig, amint láttuk, $\frac{17}{15}\frac{x}{y}$ sec kellett, tehát $\begin{array}{c}{\displaystyle y=x+\frac{17x}{15y}+\frac{17}{15}\mathrm{.}}\end{array}$ (2) (1)-et (2)-ből levonva $\begin{array}{c}{\displaystyle y-x=x-\frac{208}{15}\mathrm{,}\text{azaz}15y=30x-208.}\end{array}$ $15y$ ezen értékét (1)-be helyettesítve $\begin{array}{c}{\displaystyle x=\frac{17x}{30x-208}+\mathrm{15,}30x^2-675x+3120=0.}\end{array}$ 15-tel egyszerűsítve $\begin{array}{c}{\displaystyle 2x^2-45x+208=\mathrm{0,}\text{ahonnan}{x}_1=\mathrm{16,}\left[x_2=6\mathrm{,}5\right]\mathrm{.}}\end{array}$ A második gyök negatív $y$ értéket adna, így feladatunk megoldása $x=16$ sec, $y=\frac{272}{15}=18\frac{2}{15}$ sec. Ezek szerint a $16$ m-es $\widehat{RQ}$ út befutására $\beta$-nak $\begin{array}{c}{\displaystyle \frac{17}{15}\frac{x}{y}+\frac{17}{15}=\frac{17}{15}\left(\frac{16\cdot 15}{272}+1\right)=\frac{17}{15}\cdot \frac{32}{17}=\frac{32}{15}\text{sec-ra}}\end{array}$ volt szüksége, tehát sebessége $\begin{array}{c}{\displaystyle v_{\beta }=\frac{16\cdot 15}{32}=\frac{15}{2}=7\mathrm{,}5\text{m/sec;}}\end{array}$ $\alpha$ sebessége $\begin{array}{c}{\displaystyle v_{\alpha }=v_{\beta }\frac{y}{x}=\frac{15}{2}\cdot \frac{272}{15\cdot 16}=\frac{15}{2}\cdot \frac{17}{15}=\frac{17}{2}=8\mathrm{,}5\text{m/sec.}}\end{array}$ A pálya $s$ fél hossza annyiszorosa a $16$ méternek, mint $y$ a $\frac{32}{15}$-nek, tehát az egész pálya hossza $\begin{array}{c}{\displaystyle 2s=2\cdot 16\cdot \frac{272}{15}\cdot \frac{15}{32}=272\text{m.}}\end{array}$ II. megoldás: Válasszuk a pálya $s$ félhosszát és az $\widehat{SQ}=\widehat{QS\text{'}}=d$ távolságot (méterben mérve) ismeretlennek. Míg $\alpha$ a $\widehat{PS\text{'}}=s+d$ utat teszi meg, $\beta$ befutja a $\widehat{PS}=s-d$ utat, tehát (tekintettel arra, hogy egyenletesen fut a két futó) ugyanazon idő alatt $\alpha$ mindig $\frac{s+d}{s-d}$-szer akkora utat tesz meg, mint $\beta$. Így míg $\beta$ az $\widehat{RS}$ utat teszi meg, $\alpha$ útjára (amely $QS\text{'}=d$) $\begin{array}{c}{\displaystyle \widehat{RS}\frac{s+d}{s-d}=d\mathrm{,}\text{tehát}\widehat{RS}=d\frac{s-d}{s+d}}\end{array}$ adódik. Így $\begin{array}{c}{\displaystyle \widehat{RS}+\widehat{SQ}=d\frac{s-d}{s+d}+d=16.}\end{array}$ (1) Másrészt míg $\beta$ az $\widehat{SQ}=d$ utat futja be, $\alpha$ útja $\begin{array}{c}{\displaystyle S\text{'}T=d\frac{s+d}{s-d}\mathrm{,}}\end{array}$ és nyilván $\begin{array}{c}{\displaystyle \widehat{TP}=\frac{208}{17}\widehat{S\text{'}T}=\frac{208d\left(s+d\right)}{17\left(s-d\right)}\mathrm{.}}\end{array}$ Így $\begin{array}{c}{\displaystyle \widehat{QP}=s=d+\frac{d\left(s+d\right)}{s-d}+\frac{208d\left(s+d\right)}{17\left(s-d\right)}=d+\frac{225d\left(s+d\right)}{17\left(s-d\right)}\mathrm{.}}\end{array}$ Ebből az egyenletből meghatározhatjuk az $\frac{s}{d}=z$ arányt. $d$-vel osztva és a törtet $d$-vel egyszerűsítve $\begin{array}{c}{\displaystyle z=1+\frac{225\left(z+1\right)}{17\left(z-1\right)}\mathrm{,}17{\left(z-1\right)}^2=225\left(z+1\right)=225\left(z-1\right)+450.}\end{array}$ Innen $z-1=u$-ra $\begin{array}{c}{\displaystyle 17u^2-225u-450=0.}\end{array}$ Csak a pozitív gyök felel meg a feladatnak, tehát $\begin{array}{c}{\displaystyle u=\mathrm{15,}\frac{s}{d}=u+1=\mathrm{16,}s=16d\mathrm{,}}\end{array}$ s ezen értékét (1)-be helyettesítve $\begin{array}{c}{\displaystyle d\frac{15}{17}+d=\frac{32}{17}d=\mathrm{16,}d=\frac{17\cdot 16}{32}=\frac{17}{2}\text{m.}}\end{array}$ Így $\begin{array}{c}{\displaystyle s=16\cdot \frac{17}{2}=136\text{m,}}\end{array}$ a teljes pálya hossza pedig $\begin{array}{c}{\displaystyle 2s=272\text{m.}}\end{array}$ $\frac{17}{15}$ sec alatt $\alpha$ az $\begin{array}{c}{\displaystyle S\text{'}T=\frac{d\left(s+d\right)}{s-d}=\frac{17}{15}d=\frac{17}{15}\cdot \frac{17}{2}}\end{array}$ utat teszi meg, $\beta$ pedig $d$ utat. Így sebességük $\begin{array}{c}{\displaystyle v_{\alpha }=\frac{17}{2}=8\mathrm{,}5\text{m/sec,}{v}_{\beta }=\frac{17}{2}:\frac{17}{15}=7\mathrm{,}5\text{m/sec.}}\end{array}$ Megjegyzés: Az egyenletrendszert többféle alakban is felírhatjuk, aszerint, hogy milyen mennyiségeket választunk ismeretlennek. Az itt adott megoldások megmutatják, hogy egy a tényeket jól szemléltető vázlat megkímél fölösleges ismeretlenek bevezetésétől és megóv attól a veszélytől, hogy a köztük felállított egyenletek esetleg nem függetlenek egymástól. A versenyzők kivétel nélkül 3‐4 ismeretlennel dolgoztak. Kétségtelen, hogy az egyes egyenletek felállítása így egyrészt könnyebb, de másrészt könnyen előfordulhat ‐ és több versenyzővel meg is esett ‐ hogy a feladat valamelyik állítását kétféleképpen írjuk fel egyenlet alakjában, míg egy másik állítást figyelmen kívül hagyunk. Ez esetben is megegyezik az ismeretlenek száma az egyenletek számával, de az utóbbiak nem függetlenek egymástól, és így a végén határozatlan egyenlethez jutunk, végtelen sok megoldással. Ilyen esetben az első gondolatunk az legyen, hogy talán nem minden feltételt használtunk fel. A másodfokú egyenletrendszer megoldása bizonyos ügyességet kíván, mert a helyettesítésekkel könnyen magasabbfokú egyenletre juthatunk. Ez nem következik be abban az esetben, ha az egyik ismeretlent első fokú egyenletből fejezzük ki és a nyert elsőfokú kifejezést helyettesítjük be a másodfokú egyenletbe. Gyakorlati okokból jó, ha első pillanatra lényegtelennek látszó körülményeket sem hagyunk figyelmen kívül. Példánkban $v_{\alpha }$-ra, $v_{\beta }$-ra és $d$-re eleve kisebb számértéket várunk, mint $s$-re. Ezért, ha módunkban van, az ismeretlenek közül legelőször $s$-et küszöböljük ki, mert ha végül $v_{\alpha }$-ra, $v_{\beta }$-ra vagy $d$-re nyerünk egy másodfokú egyenletet, ez bizonyára egyszerűbb alakú lesz, mintha $s$ kiszámítására nyerünk egyenletet és így sok numerikus számítást takaríthatunk meg. Sok versenyző saját kárán jöhetett rá, hogy érdemes átgondolni ilyen mellékesnek látszó körülményeket is.   III. megoldás: A mozgási feladatokat előnyösen oldhatjuk meg grafikus úton. A vízszintes tengelyre az időt, a függőlegesre a megtett utat mérjük rá. Az út és idő összetartozó értékeit pontokkal ábrázoljuk; e pontok összessége a mozgás grafikonja. Az egyenletes mozgás grafikonja egyenes vonal. Az idő-tengellyel bezárt szögének tangense a mozgó test sebességét adja meg. Példánkban az út-tengelyre a pályát kiegyenesítve rakjuk rá, kezdőpontja és a végpontja egyaránt $P$ (utóbbit a 2. ábrán $P^{*}$-gal jelöltük), a táv felezési pontja $Q$. A távot és a mozgások sebességét nem ismerjük, ezért csak vázlatszerű grafikont tudunk készíteni, amelyről az ismeretlenek számértékét nem fogjuk tudni közvetlenül leolvasni, de könnyű lesz azokat kiszámítani a vázlatszerű grafikonról is leolvasható egyszerű összefüggésekből. $\alpha$ mozgását a $P$ pontból kiinduló ugyancsak $\alpha$-val jelölt egyenessel ábrázoljuk; $\beta$ sebessége kisebb, ezért a mozgását az $\alpha$-nál kevésbé meredek $\beta$ egyenes ábrázolja (2. ábra). 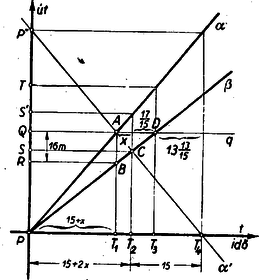    2. ábra   $T_1$ időpontban, mikorra $\alpha$ megtette a táv felét. $\beta$ hátrább van $16$ m-rel, melyet függőlegesen bejelöltünk: $AB=16$ m. A tükrös helyzet időpontja $T_2$, amikor $\beta$ helyzetét a $C$ pont jellemzi. A $C$ pontot $\alpha$ tükörképe az $\alpha \text{'}$ egyenes metszi ki a $\beta$ egyenesből. $\beta$ a táv felét $T_3$ időpontban éri el. Ennek a helyzetnek a grafikonon a $D$ pont felel meg, amelyben a $\beta$ egyenes metszi a $Q$-n átmenő, $t$ idő-tengellyel párhuzamos $q$ egyenest. $\alpha$ célbaérésének időpontját $T_4$-gyel jelöltük. Ez a pont az időtengelyen a $P$ kezdőponttól kétszer akkora távolságra van, mint $T_1$ és az $\alpha \text{'}$ egyenes keresztül megy $T_4$-en. Az időkülönbségeket a $q$ középvonalon tüntettük fel: $T_2-T_1$-et $x$-szel jelöltük, a feladatból ismert $T_3-T_2=\frac{17}{15}$, $T_4-T_3=13\frac{13}{15}$, $T_4-T_2=15$, $T_1-0=T_4-T_1=$ $=15+x$. A $t$ és a vele párhuzamos $q$ egyenes metszi a $C$ ponton átmenő egyeneseket. Tekintsük a metszéspontokat megfelelő pontoknak és a megfelelő pontok által határolt egyenes szakaszokat megfelelő szakaszoknak. (Tehát $A$-nak megfelel $T_4$ pont, $D$-nek megfelel $P$; az $AD$ szakasznak megfelel a $T_{4}P$ szakasz.) A megfelelő szakaszok aránya egyenlő, tehát $\begin{array}{c}{\displaystyle x:15=\frac{17}{15}:\left(15+2x\right)\mathrm{,}\text{átalakítva}2x^2+15x-17=0.}\end{array}$ Ennek az egyenletnek egyik gyöke $x=1$, a másik negatív, tehát a feladat szerint értelmetlen. Ezután $x$ segítségével az ismeretleneket az ábrából tüstént kifejezhetjük és kiszámíthatjuk. $\beta$ sebességét $v_{\beta }$-t (a $\beta$ egyenes emelkedési szögének tangensét) az $ADB$ derékszögű háromszögből határozhatjuk meg: $\begin{array}{c}{\displaystyle v_{\beta }=\frac{16}{x+\frac{17}{15}}=\frac{16}{1+\frac{17}{15}}=\frac{240}{32}=7\mathrm{,}5\text{m/sec.}}\end{array}$ A $PD{T}_3$ derékszögű háromszögből a táv fele: $\begin{array}{c}{\displaystyle s=D{T}_3=P{T}_3\cdot v_{\beta }=\left(15+2x+\frac{17}{15}\right)\cdot 7\mathrm{,}5=136\text{m.}}\end{array}$ Végül a $PA{T}_1$ derékszögű háromszögből, $\alpha$ sebessége: $\begin{array}{c}{\displaystyle v_{\alpha }=\frac{A{T}_1}{P{T}_1}=\frac{s}{15+x}=\frac{136}{16}=8\mathrm{,}5\text{m/sec.}}\end{array}$ Feladatunkat ezzel megoldottuk és a hosszúság-egység és idő-egység megválasztása után a két mozgást grafikusan, léptékhelyesen is ábrázolhatjuk.