Kezdőlap


Feladat:	1954. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1954/október, 37 - 38. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Háromszögek hasonlósága, Thalesz-kör, Pont körüli forgatás, Középponti és kerületi szögek, Tengelyes tükrözés, Arany Dániel
Hivatkozás(ok):	Feladatok: 1954/szeptember: 1954. évi Arany Dániel matematikaverseny 2. forduló kezdők (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Adva van az $A B C D$ húrnégyszögnek $A B = A D = a$ , $B C = b$ és $C D = c$ oldala. Képzeljük a feladatot megoldottnak (1. ábra).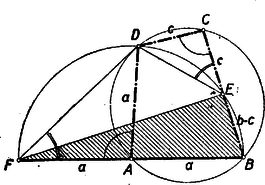

1. ábra

A

körül

A B = A D = a

sugárral rajzolt kör kimetszi a

B C

oldalból, vagy annak meghosszabbításából az

E

pontot, az

A B

oldal meghosszabbításából az

F

pontot. Ismeretes, hogy a húrnégyszögnek bármely szöge egyenlő a szemközti szög mellékszögével. Eszerint tehát a

C

-nél fekvő egy íves szög egyenlő az

A

-nál fekvő egy íves szöggel és az

F B E D

húrnégyszögben az

F

-nél fekvő két íves szög egyenlő a

E

-nél fekvő két íves szöggel. Ebből következik, hogy a

D A F

és

D C E

háromszögek 2‐2 szöge egyenlő, vagyis e két háromszög hasonló. De

A D = A F = a

, és így

C D = C E = c

, vagyis

B E = b - c

. Thales tétele értelmében

B E F ∢ = 90^{\circ}

.
Az

F B = 2 a

átfogóból és

B E = b - c

befogóból a

B E F

derékszögű háromszög (az 1. ábrán srafozva) egyszerűen megszerkeszthető, feltéve, hogy

2 a > b - c

. A

B E F

derékszögű háromszög birtokában az

A

C

és

D

pontok megszerkesztése már nem okoz nehézséget.

II. megoldás: Képzeljük a feladatot megoldottnak. A jelöléseket megtartva, forgassuk az

A D C ▵

-et

A

pont körül úgy, hogy a

D

pont

D'

elforgatása

B

-be kerüljön (2. ábra).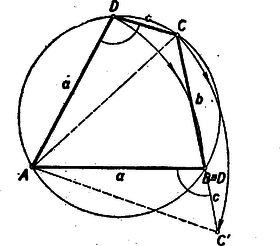

2. ábra

Mivel húrnégyszögünk egy íves

D ∢

-e egyenlő a szemközti

B ∢

egy ívvel jelzett mellékszögével, azért a

C

pont elforgatása,

C'

C B

oldal meghosszabbítására kerül. Mivel

A C = A C'

, azért az

A

pont egyrészt rajta van a

C C'

távolságot merőlegesen felező egyenesen, másrészt pedig a

B

középpontú

a

sugarú körön. A szerkesztést a 3. ábra mutatja.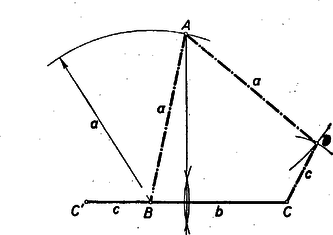

3. ábra

Megoldás van, ha

a > \frac{b - c}{2}

, vagyis

2 a > b - c

III. megoldás: Képzeljük a feladatot megoldva és használjuk az eddigi jelöléseket. Nem megy az általánosság rovására, ha feltesszük, hogy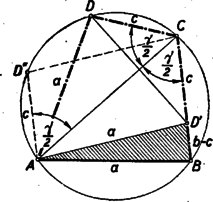

b > c

(4. ábra).

4. ábra

A B = A D

, tehát a fölöttük levő

C

-t nem tartalmazó körívek is egyenlők. Így a kerületi szögek tétele alapján a

C A

átló felezi a

C

-nél fekvő

γ

szöget, tehát a

D

pontnak az

A C

átlóra vonatkozó tükörképe

D'

ráesik a

b

oldalra és

B D' = b - c

. (

D'

tehát azonos az I. megoldásban szerepelt

E

ponttal). Az

A B D'

egyenlőszárú háromszög (a 4. ábrán srafozva) az

a

és

b - c

szakaszokból könnyen megszerkeszthető. (E háromszögnek a keresett húrnégyszöggé való kiegészítése már triviális.)
Lényegében ugyanennek a háromszögnek megszerkesztésére vezet, ha

D

-nek megszerkesztjük az

A C

átlót merőlegesen felező egyenesre vonatkozó

D''

tükörképét (4. ábra). Mivel a

C A D'' ∢

a tükrözés folytán

\frac{γ}{2}

, azért a váltószögek törvénye alapján

A D'' ∥ B C

, vagyis

B C D'' A

egyenlőszárú trapéz, amely az adatokból (

a

szár,

b ∥ c

) szerkeszthető. A szerkeszthetőség feltétele, hogy

2 a > b - c