Kezdőlap


Feladat:	1954. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1954/november, 82 - 86. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Háromszögek hasonlósága, Szögfüggvények, síkgeometriai számítások, Egyenlő szárú háromszögek geometriája, Középponti és kerületi szögek, Arany Dániel
Hivatkozás(ok):	Feladatok: 1954/szeptember: 1954. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Nem megy az általánosság rovására, ha egyszer és mindenkorra feltételezzük, hogy $a > b$ . Pythagoras tétele szerint

\begin{matrix} a^{2} + b^{2} = c^{2}, \end{matrix}

(1)

feltételünk szerint (mivel a súlyvonal

\frac{c}{2}

)

\begin{matrix} 2 a b = \frac{c^{2}}{2} \end{matrix}

(2)

(1) és (2)-t összeadva, ill. kivonva nyerjük

\begin{matrix} {(a + b)}^{2} & = \frac{3 c^{2}}{2}, \\ {(a - b)}^{2} & = \frac{c^{2}}{2}, \end{matrix}

amiből

\begin{matrix} a + b & = \frac{c \sqrt[]{3}}{\sqrt[]{2}} = \frac{c \sqrt[]{6}}{2}, & (3) \\ a - b & = \frac{c \sqrt[]{2}}{2} & (4) \end{matrix}

A szerkesztés ezek alapján többféleképpen is történhetik.

α

) (3) és (4) összeadásából nyerjük, hogy

a = \frac{c \sqrt[]{6} + c \sqrt[]{2}}{4}

, amely szakasz könnyen szerkeszthető (

c \sqrt[]{6}

mértani középarányos

2 c

és

3 c

között,

c \sqrt[]{2}

pedig

c

és

2 c

között).

a

és

c

birtokában a keresett háromszög szerkesztése triviális.

β

) (3) alapján

a + b

, mint mértani középarányos

c

és

\frac{3}{2} c

között megszerkeszthető. Az

a + b

és

c

szakaszok birtokában a háromszög szerkesztése a tankönyvből ismeretes (1. ábra).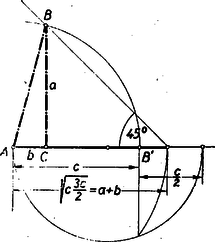

1. ábra

γ

) (4) szerint

a - b

olyan négyzet átlója, melynek oldala

\frac{c}{2}

a - b

és

c

birtokában a derékszögű háromszög ismert módon (2. ábra) megszerkeszthető.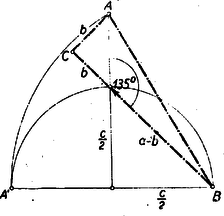

2. ábra

Mindhárom esetben könnyen kimutatható, hogy az így megszerkesztett háromszög tényleg eleget tesz követelményünknek. Pl. az utóbbi esetben Pythagoras-tétele alapján

\begin{matrix} {(a - b)}^{2} = a^{2} + b^{2} - 2 a b = 2 \cdot \frac{c^{2}}{4} = \frac{c^{2}}{2}, \end{matrix}

amiből

\begin{matrix} 2 a b = a^{2} + b^{2} - \frac{c^{2}}{2} = c^{2} - \frac{c^{2}}{2} = \frac{c^{2}}{2}, \end{matrix}

és így tényleg

\begin{matrix} a b = \frac{c^{2}}{4} . \end{matrix}

Oldalak helyett szögeket is kiszámíthatunk, mint azt az alábbi II‐V. megoldások mutatják.

II. megoldás: Képzeljük a feladatot megoldottnak. A betűzést a 3. ábra mutatja.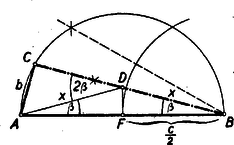

3. ábra

Jelöljük az

A B

átfogó felező pontját

F

-fel, tehát

F A = F B = \frac{c}{2}

. Az

F

-ben az átfogóra emelt merőleges messe a

B C = a

befogót

D

-ben. Legyen

A D = D B = x

.
A szögek egyenlősége miatt

\begin{matrix} A B C ▵ \sim D B F ▵, \end{matrix}

és így

\begin{matrix} x : \frac{c}{2} = c : a, \end{matrix}

amiből

\begin{matrix} x = \frac{c^{2}}{2 a} . \end{matrix}

De a feltétel szerint

\begin{matrix} c^{2} = 4 a b, \end{matrix}

és így

\begin{matrix} x = 2 b \end{matrix}

A C D

derékszögű háromszögben

sin C D A ∢ = sin 2 β = \frac{b}{x} = \frac{b}{2 b} = \frac{1}{2}

, amiből

\begin{matrix} 2 β = 30^{\circ}, vagyis β = 15^{\circ}, \end{matrix}

mely szög könnyen szerkeszthető.

III. megoldás: A jelöléseket megtartva

\begin{matrix} a = c sin α, b = c cos α . \end{matrix}

A feltétel szerint

\begin{matrix} a b = c^{2} sin α cos α = \frac{c^{2}}{4}, \end{matrix}

vagyis,

\frac{2}{c^{2}}

-tel szorozva

\begin{matrix} 2 sin α cos α = \frac{1}{2}, \end{matrix}

azaz

\begin{matrix} sin 2 α = \frac{1}{2}, \end{matrix}

ahonnan

(0 < 2 α < 180)

\begin{matrix} 2 α = 30^{\circ} ill. 150^{\circ}, \end{matrix}

a > b

miatt

\begin{matrix} α = 75^{\circ} . \end{matrix}

IV. megoldás: Az előbbi jelöléseket megtartva jelöljük az

A F C ∢

-et

φ

-vel (4. 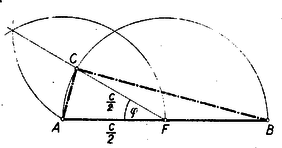ábra).

4. ábra

A F C ▵

területe a fele az

A B C ▵

területének. Tehát

\begin{matrix} \frac{1}{2} \cdot \frac{c}{2} \cdot \frac{c}{2} sin φ = \frac{a b}{4}, \end{matrix}

vagyis

c^{2} sin φ = 2 a b

, amiből

sin φ = \frac{2 a b}{c^{2}}

.
De a feltétel szerint

a b = \frac{c^{2}}{4}

, vagyis

2 a b = \frac{c^{2}}{2}

, és így

sin φ = \frac{1}{2}

, vagyis

φ = 30^{\circ}

. A

C

pont megszerkesztése a körülírt körön egyszerűbb már nem lehet.

V. megoldás: A legegyszerűbb megoldáshoz (ha nem is a legegyszerűbb szerkesztéshez) jutunk, ha feltételünket >>helyesen<< olvassuk.
Feltételünk szerint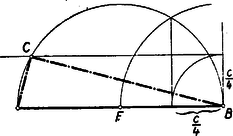

\begin{matrix} a b = \frac{c^{2}}{4} = c \cdot \frac{c}{4} . \end{matrix}

a b

a háromszög kétszeres területe, tehát

c \cdot \frac{c}{4}

is az, vagyis

\frac{c}{4}

a háromszögnek az átfogóhoz tartozó magassága. A szerkesztést az 5. ábra mutatja.

5. ábra

Az utóbbi megoldásnál közvetlenül nyilvánvaló, hogy a megszerkesztett háromszög teljesíti a feladatban kirótt feltételt:

a b = c \cdot \frac{c}{4} = \frac{c^{2}}{4}

. A II‐IV. megoldásnál (ahol tulajdonképpen kiszámítottuk, hogy

α = 75^{\circ}

és

β = 15^{\circ}

) a következőképpen igazolhatjuk szerkesztésünk helyességét:

\begin{matrix} a = c cos 15^{\circ}, b = c sin 15^{\circ}, \end{matrix}

és így

\begin{matrix} a b = c^{2} sin 15^{\circ} cos 15^{\circ} = c^{2} \frac{sin 30^{\circ}}{2} = \frac{c^{2}}{4} . \end{matrix}

De anélkül, hogy a háromszög oldalait vagy szögeit kiszámítanánk, is megoldhatjuk feladatunkat, amint azt az alábbi VI‐VII. megoldások mutatják.

VI. megoldás: Képzeljük a feladatot megoldottnak. A betűzést a 6. ábra mutatja.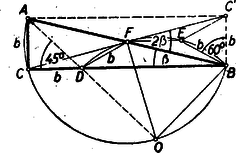

6. ábra

Szerkesszük meg azt a kört, amely a

C F

egyenest

F

-ben érinti és a

B

csúcsponton is átmegy. Legyen ennek a körnek középpontja

O

és messe ez a kör a

B C

befogót másodszor

D

-ben. Mivel

C F^{2} = C B \cdot C D

, vagyis

{(\frac{c}{2})}^{2} = a \cdot C D

, azért a feladat szerint

C D = b

. Ha kimutatjuk, hogy

O

rajta van az

A B

fölé, mint átmérő fölé rajzolt körön és

B O = \frac{c}{2}

, továbbá, hogy a

D

pont rajta van az

A O

egyenesen, akkor lényegében a II. megoldásban nyert szerkesztéshez jutottunk, de más indokolással.
Mivel

B F C

egyenlőszárú háromszögből

\begin{matrix} F C D' ∢ = F B D ∢ = β, \end{matrix}

másrészt

C F D ∢ = β

, mint az

\hat{F D}

ív fölötti húr-érintőszög, azért

C D F

egyenlő szárú háromszög és

\begin{matrix} F D = C D = b . \end{matrix}

\hat{F B}

ívhez tartozó húr-érintő szög, mint a

B F C ▵

külső szög

2 β

, tehát ez az ív kétszerese az

\hat{F D}

ívnek. Az

E

felezőpontját berajzolva, a húrokra

F E = E B = b

és

F E ∥ D B

.
Az

A B C ▵

-et téglalappá egészítve ki

F E

ennek a középvonalán fekszik. Így

C' E = E B = b

, másrészt

B C' = A C = b

, tehát a

B E C'

szabályos háromszögből

C' B E ∢ = 60^{\circ}

, s így

\begin{matrix} E B D ∢ = 2 β = 30^{\circ}, \end{matrix}

Ugyanekkorák az

\hat{F B}

íven nyugvó kerületi szögek, és így a középponti szög

\begin{matrix} B O F ∢ = 60^{\circ} és B O = F O = B F = \frac{c}{2} \end{matrix}

a kör sugara. A

B O D

egyenlőszárú háromszög alapján nyugvó szög

\begin{matrix} D B O ∢ = 60^{\circ} - β = 60^{\circ} - 15^{\circ} = 45^{\circ} = B D O ∢ . \end{matrix}

Ebből következik, hogy ez a háromszög derékszögű, továbbá

A

D

és

O

egy egyenesbe esnek és

O

C

-vel együtt) az

A B

fölötti félkörön van.
Eszerint a szerkesztés menete: az

A B = c

átmérő fölötti félkört a

B O = \frac{c}{2}

távolsággal elmetszve, majd az

A O

egyenest az

O D = \frac{c}{2}

távolsággal elmetszve, a

B D

egyenes metszi ki az

A B

fölötti félkörből a keresett háromszög

C

csúcsát.
A szerkesztés igazolása: Mivel az

A B O ▵

szögei

30^{\circ}

60^{\circ}

és

90^{\circ}

, azért az

O

körüli

\frac{c}{2}

sugarú körnek az

A B

-vel való

F

metszéspontjára

F O B ▵

szabályos, mert

F B O ∢ = 60^{\circ}

, tehát

F

felezőpont,

C F = \frac{c}{2}

, mint a derékszögű háromszög súlyvonala, továbbá

B F O ∢ = 60^{\circ}

B O D

egyenlőszárú derékszögű háromszög, tehát

A D C ∢ = D A C ∢ = 45^{\circ}

C D = C A = b

; másrészt az

A F C

egyenlőszárú háromszögben

C A F ∢ = 45^{\circ} + 30^{\circ} = 75^{\circ}

, s így az

A F C ∢ = 30^{\circ}

. Ebből következik, hogy

\begin{matrix} C F O ∢ = 180^{\circ} - 30^{\circ} - 60^{\circ} = 90^{\circ} . \end{matrix}

Így

C F

érinti az

O

középpontú kört, s így

\begin{matrix} C F^{2} = C D \cdot C B = b a, \end{matrix}

tehát az

A B C ▵

megfelel a kívánalmaknak.

VII. megoldás: Az adott

A B = c

átfogó fölé rajzolt

F

középpontú Thales-körben az

A B

átmérőre merőleges sugár végpontját jelöljük

O

-val (7. ábr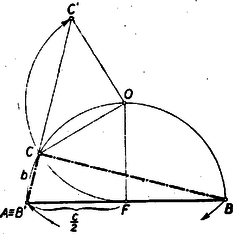a).

7. ábra

O

körül

O F = \frac{c}{2}

sugárral rajzolt kör metszi ki a Thales-körből a keresett

C

pontot. (Ez tulajdonképpen az V. megoldásban nyert szerkesztés, ismét más megindokolással.)
Forgassuk el a

B C = a

befogót

O

körül

90^{\circ}

-kal az óra járásával megegyező irányban, akkor a

B

elforgatása a

B'

A

pontba kerül,

C

elforgatása pedig

C'

, és

B' C' \equiv A C' ⊥ B C

. Mivel

A C

is merőleges

B C

-re, azért a

C'

pont az

A C

befogó meghosszabbításán fekszik.
A szerkesztés szerint az

A F = \frac{c}{2}

O

körül rajzolt körnek az

A

pontból húzott érintője, és így

\begin{matrix} A C' \cdot A C = a b = {(\frac{c}{2})}^{2} . \end{matrix}