Feladat: 1954. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 1. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1954/október, 33 - 35. oldal  PDF  |  MathML 
Témakör(ök): Kör (és részhalmaza), mint mértani hely, Középponti és kerületi szögek, Pont körüli forgatás, Arany Dániel
Hivatkozás(ok):Feladatok: 1954/szeptember: 1954. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Legyen A és B a két rögzített pont, F1 és F2 az AB húrra merőleges átmérőnek végpontjai és C a harmadik csúcs, mely egyelőre mozogjon az AF2B köríven (1. ábra).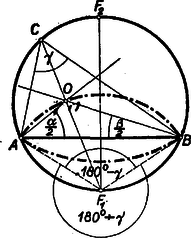

 
 
1. ábra
 

A kerületi szögek tétele alapján az ACB∢=γ szög állandó. A beírt kör O középpontja a szögfelezők metszéspontja, így az
AOB▵-ből az  AOB∢=180∘-α+β2=180∘-180∘-γ2=90∘+γ2,
vagyis az O pontból az AB húr az állandó 90∘+γ2 szög alatt látszik. Tehát az O pontok mértani helyének egy része az AB húrhoz tartozó, 90+γ2 szögnek megfelelő látókörív. E látókörív középpontja az AB húrra merőleges F1F2 egyenesnek az a pontja, amelyben az ugyanazon íven nyugvó középponti szög 2(90+γ2)=180∘+γ, vagyis amelyből az AB húr 360∘-(180∘+γ)=180∘-γ szög alatt látszik; ez a pont pedig az F1 pont, mert az ACBF1 húrnégyszögben az AF1B∢=180∘-γ, mint a γ szöggel szembenfekvő szög.
Ugyanúgy kimutatható, hogy ha a C pont a BF1A íven mozog, akkor az O pont leírja az F2 középpontú BA ívet. Tehát a feltételeket kielégítő O pontok szükségképpen az F1 és F2 középpontú, a kör belsejében fekvő, AB köríveken fekszenek. Meg kell még mutatnunk, hogy ‐ fordítva ‐ e köríveknek minden pontja eleget tesz a követelményeknek. Az AOB∢=90∘+γ2 szög AO, ill. BO szárára tükrözzük az AB egyenest (1. ábra). A tükörképek az AB egyenessel, annak az F2-t tartalmazó oldalán 2⋅OAB∢ és 2⋅OBA∢ nagyságú szögeket zárnak be. E két szög összege
2(OAB∢+OBA∢)=2[180∘-(90∘+γ2)]=180∘-γ
tompaszög, tehát ezek az egyenesek metszik egymást az AB határolta, F2-t tartalmazó félsíkban és γ nagyságú szöget zárnak be. Ezek szerint C metszéspontjuk rajta van az AF2B köríven és O, mint két szögfelező metszéspontja, az ABC▵ beírt körének középpontja, tehát megvan a mértani helyet definiáló tulajdonsága.
Most már kimondhatjuk, hogy a keresett mértani hely: az F1 és F2 középpontú, a kör belsejében fekvő, AB^ körívek.
 

II. megoldás: Ha C1≡F2, akkor az AC1B▵-be írt kör középpontja legyen 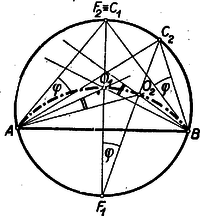O1 (2. ábra).
 
 
2. ábra
 

Az AF2B körív egy tetszőleges C2 pontjához tartozó ABC2▵ beírt körének középpontja, vagyis szögfelezőinek metszéspontja legyen O2. A változó C csúcspontból kiinduló szögfelező, a kerületi szögek tétele alapján, mindenkor átmegy az F1 ponton
C1AC2∢=C1F1C2∢=C1BC2∢=φ,
mint ugyanazon a köríven (C1C2^) nyugvó kerületi szögek.
Ebből következik, hogy ha a háromszög fc szögfelezője F1 körül φ szöggel elfordul, akkor
1. az a és b oldal is φ szöggel fordul el és következésképpen
2. a másik két szögfelező φ2 szöggel (az ábrán kétszeres ívvel jelölve) fordul el.
Tehát
O1AO2∢=O1BO2∢=φ2.

Mivel a kerületi szögek tétele megfordítható, ez azt jelenti, hogy az O1 és O2 pontok rajta vannak azon az AB^ köríven, melynek az O1O2 ívhez tartozó középponti szöge 2⋅φ2=φ, és maga a középpont pedig rajta van az AB húrt merőlegesen felező F1F2 egyenesen. Mivel ‐ mint láttuk ‐ éppen O1F1O2∢=φ, azért az O pontokat tartalmazó AB^ körív középpontja F1. A fenti bizonyítás megfordításával kimutatható, hogy a szóbanforgó körív minden pontja eleget tesz feltételeinknek.
Ugyanígy végezhető a bizonyítás az AF1B körívre nézve.
 

III. megoldás: F1AB∢=F1CB∢=γ2, mint kerületi szögek (3. ábra).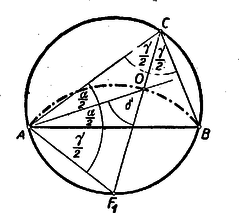
 
 
3. ábra
 

Az AOC▵ O-nál fekvő külső szöge δ egyenlő a két belső szög összegével, vagyis δ=α2+γ2, amiből következik, hogy az AOF1▵ egyenlő szárú, tehát
F1O=F1A.
Ugyanígy végezhető a szükségesség e bizonyítása az AF1B^ köríven fekvő C pontokhoz tartozó O pontokra nézve is. E bizonyítások megfordításból következik, hogy a szükséges feltétel elégséges is, és ezzel bebizonyítottuk, hogy az O pontok mértani helye az F1, és F2 középpontú, A (és B) ponton átmenő köröknek, az adott kör belsejébe eső ívei.