Kezdőlap


Feladat:	1953. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1953/október, 38 - 40. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Pont körüli forgatás, Háromszögek egybevágósága, Arany Dániel
Hivatkozás(ok):	Feladatok: 1953/szeptember: 1953. évi Arany Dániel matematikaverseny 1. forduló haladók (speciális) 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A leírás különböző ábrákhoz vezethet (1., 2. és 3. ábra), aszerint, hogy hol vesszük fel az $E$ pontot. Az 1. ábrán a $B D$ a 2.-on $D A$ negyedkörön vettük az $E$ pontot. A két ábrán, csak a trapéz helyzete tükrös egymáshoz képest az $A B$ átmérőre vonatkozóan. Ez a területekre nincs befolyással. Ha ellenben $E$ átjut az $A C$ ívre (3. ábra), akkor az $A B F G$ négyszög hurkolt négyszög két párhuzamos oldallal: >>hurkolt trapéz<<.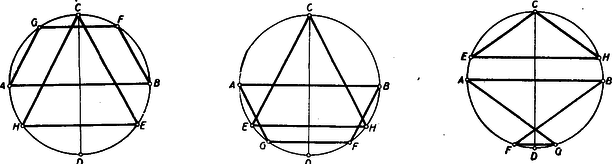

1. ábra 2. ábra 3. ábra

Az állítás erre az esetre is igaz, ha a hurkolt trapéz területét megfelelően értelmezzük, de hogy egyáltalán mit értsünk egy önmagát metsző négyszög területén, az eleve nem világos és ezért hibáztatható is a feladat megfogalmazása.
Az

A B G F

trapéz területét venni, vagy akár a két háromszög területének összegét, ez a feladat szempontjából nem megfelelő, hiszen a keletkezett kettős háromszögből az

A B

oldalhoz csatlakozó hasonló a

C E H

háromszöghöz, de már egymagában is nagyobb nála, mert

A B > E H

. Hogy a terület milyen értelmezése mellett érvényes az állítás ebben az esetben is, az bizonyítás közben fog adódni. Ha

E

C B

ívre kerül, akkor lényegesen új esetet nem kapunk, csak a >>hurkolt trapéz<< kerül ismét az

A B

átmérő másik partjára. Térjünk ezután a feladat megoldására.

I. megoldás: Alakítsuk először a trapézt téglalappá úgy, hogy az

F

-ből

A B

-re bocsátott

F K

merőlegessel elvágott

B F K

háromszöget a

G A

oldalhoz illesztjük (4. ábra).

4. ábra

Az így keletkezett

A M F K

téglalapot az

A F

átlóval két egyenlő részre osztjuk, és megmutatjuk, hogy a keletkezett

A F K ▵

egybevágó a

C E H

háromszög felét kitevő

C E L

háromszöggel, ahol

L

E H

húr középpontja (mely nyilván

C D

-re esik). Valóban forgassuk el utóbbit a kör középpontja körül az óra járásával ellenkező irányban

90^{\circ}

-kal. Ekkor

C

átmegy

A

-ba és mivel

D

az elforgatás után

B

-be kerül, így

L

A B

átmérőre fog kerülni. Azt kell csak belátnunk, hogy az

E

pont

F

-be megy át, ez pedig teljesül, mert a

B C

és

E F

ívet párhuzamos húrok metszik ki a körből, tehát az

E F

ív is negyedkör.
A bizonyítás lényegtelen változtatással alkalmazható arra az esetre is, ha

E

B D

negyedkörön van (a következő megoldásból látható lesz, hogy hogyan), nem világos azonban, hogy hogyan vihető át a hurkolt esetre. Ez sokkal könnyebben lesz látható a következő megoldásból, amely szoros rokonságban van az elsővel.

II. megoldás: Az előbbi jelöléseket használva (4. ábra) nyilvánvaló, hogy

A K

a trapéz középvonalával egyenlő, tehát a trapéz ill. háromszög

t_{1}

ill.

t_{2}

területe

\begin{matrix} t_{1} = A K \cdot F K, t_{2} = \frac{C L \cdot E H}{2} = C L \cdot E L . \end{matrix}

Megmutatjuk, hogy

\begin{matrix} F K = E L és A K = C L, \end{matrix}

ill. utóbbi helyett, hogy

B K = D L

. Mindkét egyenlőség következik abból, hogy

\begin{matrix} B F K ▵ ≅ D E L ▵ . \end{matrix}

Forgassuk el az utóbbi háromszöget

90^{\circ}

-kal az óra járásával ellenkező irányban a kör középpontja körül. Ekkor

D

átmegy

B

-be,

E L

pedig a

B

-hez húzott sugárra merőleges helyzetbe kerül,

E

pedig átmegy

F

-be, amint azt az I. megoldásban láttuk. Ezzel állításunkat igazoltuk.

Megjegyzés: A bizonyítás >>hurkolt trapéz<< (5. ábra) esetén is azt adja, hogy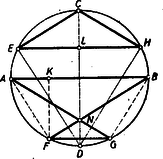

\begin{matrix} E L = F K, D L = B K, amiből C L = A K, \end{matrix}

tehát

\begin{matrix} E L \cdot C L = F K \cdot A K = F K . \frac{A B - F G}{2} = \frac{F K \cdot A B}{2} - \frac{F K \cdot F G}{2} . \end{matrix}

5. ábra

Baloldalt ismét a

C E H ▵

területe áll, a jobboldal viszont felfogható az

A F B

és

A F G

háromszögek területei különbségének. Ebből a különbségből kiesik a két háromszög közös részének a területe és marad a >>hurkolt trapéz<< nagyobb és kisebb háromszöge területének különbsége. A hurkolt esetben tehát e területkülönbség egyezik meg a

C E H

háromszög területével.
Számítás nélkül is bebizonyíthatjuk ezt az eredményt. Ugyanis a közönséges trapézra fentebb már bebizonyított tétel alapján az 5. ábrában a

D E H ▵

területe egyenlő az

A B G F

közönséges trapéz területével, továbbá ugyancsak az előbbiek alapján

A B F ▵ ≅ C D E ▵ ≅ C D H ▵ ≅ B G A ▵

.
Tehát (területekről beszélve)

\begin{matrix} C E H = C E D H - D E H = C E D H - A B G F = \\ = C E D H - (A B F + A B G - A B N + F G N) = \\ = C D E + C D H - A B F - A B G + A B N - F G N = A B N - F G N . \end{matrix}

Könnyű a feladatot úgy fogalmazni, hogy a kettősség ne is lépjen fel. (L. 4. és 5. ábrát). Ha a

B F

és

A G

egyenesek metszéspontját mindenkor

N

-el jelöljük, akkor a

C E H

háromszög területe ‐ minden esetben ‐ az

A B N

és

G F N

háromszögek területének különbségével egyenlő.
A III. osztályosok más szempontból is érthetőnek fogják tartani a nyert eredményt. A koordináta-geometriában ugyanis kiderült, bizonyos szempontból előnyös lehet a területet előjeles mennyiségnek tekinteni, oly módon, hogy minden idomhoz megadjuk, hogy hogyan járjuk körül a kerületét (sokszögeknél ez például a csúcsok sorrendjével már meg van adva) és akkor azon idomok területét, melyek körüljárásban a jobbkezünk felé esnek, ellenkező előjelűnek nevezzük, mint amelyek körüljáráskor balról fekszenek. (Bármelyik lehet pozitív, de a másik minden esetben negatív lesz.) Ilyen értelmezés mellett hurkolt négyszög területéül mindig azon két háromszög területének különbsége adódik, melyekből a hurkolt négyszög áll.

III. megoldás: Mivel mindkét szóban forgó idom tükrös a

C D

átmérőre, mint tengelyre, így elég azt megmutatni, hogy a háromszög fele és a trapéz fele egyenlő területű, tehát ha az

F G

és

E H

húrok felezőpontjai

J

és

L

(6. ábra), akkor azt kell megmutatnunk, hogy a

C E L

háromszög és a

B F J O

trapéz egyenlő területű.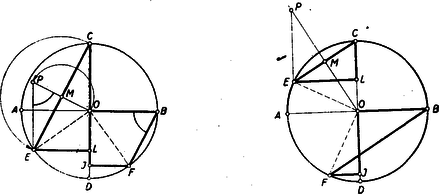

6. ábra 7. ábra

Húzzuk meg az

E C

húr

O M

felező merőlegesét és forgassuk a

C M O

háromszöget az

M

pont körül az

E M

szakasz mellé. Az így keletkezett

E L O P

derékszögű trapézban

\begin{matrix} E P O ∢ = O B F ∢ \end{matrix}

mint merőlegesszárú szögek, mert

P O

merőleges a

C E

-vel párhuzamos

B F

húrra is.

E P

és

O B

, a trapézok hosszabb párhuzamos oldalai sugárnyi hosszúságúak és ugyancsak sugárnyi hosszúságú az

E O

ill.

O F

átló is. Így a

B F J O

trapéz egybevágó, tehát egyenlő területű is, a

P O L E

trapézzal, tehát egyenlő területű a

C E L

háromszöggel is.
A hurkolt esetben is igaz, hogy az

C E O

háromszög átalakítható a

P E O

háromszöggé (7. ábra) és utóbbi egybevágó a

B O F

háromszöggel. Viszont előbbiből most el kell hagyni az

E L O

háromszöget, hogy a

C E L

háromszöget kapjuk. Ennek megfelelően

B F O

-ból

O J F

-fel egyenlő területet kell elvennünk. A közös rész elhagyása után a hurkolt négyszög

O B

-hez csatlakozó nagyobb háromszöge marad meg. Ebből kell még az

F J

-hez csatlakozó kisebb háromszöget elvenni, hogy

C E L

-lel egyenlő területet kapjunk.