Feladat: 1953. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1953/október, 35 - 36. oldal  PDF  |  MathML 
Témakör(ök): Trapézok, Alakzatba írt kör, Érintőnégyszögek, Négyszögek középvonalai, Arany Dániel
Hivatkozás(ok):Feladatok: 1953/szeptember: 1953. évi Arany Dániel matematikaverseny 1. forduló kezdők (speciális) 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: a) Tegyük fel, hogy a szárak fölé rajzolt körök érintkeznek. (1. ábra)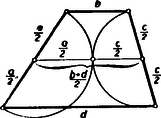

 
 
1. ábra
 

Ekkor a körök centrálisának hossza a sugarak összege, vagyis a szárak összegének a fele. Másrészt viszont a centrális éppen a trapéz középvonala, tehát hossza a párhuzamos oldalak összhosszának a fele. A feltételnek megfelelő trapézban tehát a szemközti oldalpárok összhossza megegyezik és tudjuk, hogy ha ez egy konvex négyszögre teljesül, akkor abba az oldalakat érintő kör írható. Tehát a feltétel elégséges.
b) Ha a trapézba az oldalakat érintő kör írható, akkor tudjuk, hogy a szemközti oldalpárok összege megegyezik s így a középvonal, melynek hossza a párhuzamos oldalak számtani közepe, egyben a szárak felének összegével is egyenlő s így a szárak mint átmérők fölé rajzolt körök közös pontban metszik a centrálist. De ha két körnek a centrálisukon van közös pontja, akkor e pontban érintkeznek. Tehát a feltétel szükséges is. Ezzel igazoltuk a bizonyítandó állítást.
 

II. megoldás: Tetszés szerinti ABCD trapéz (BC||AD) AB szára fölé rajzoljunk félkört. Messe ez a középvonalat E-ben (2. ábr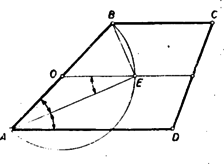a).
 
 
2. ábra
 

Ekkor E-n mennek át az A és B csúcsból húzott szögfelezők. Valóban, a félkör középpontját O-val jelölve AOE▵, egyenlő szárú s így OAE∢=OEA∢, mivel pedig a középvonal párhuzamos a párhuzamos oldalakkal, így OEA∢=EAD∢, tehát AE felezi az A-nál lévő szöget. Hasonlóan látható, hogy BE szögfelező.
A trapézba akkor és csakis akkor írható kör, ha a négy szögfelező egy ponton megy keresztül, tehát akkor és csakis akkor, ha a szárak fölé rajzolt köröknek közös pontja van a középvonalon, tehát ha e körök érintkeznek.
Egyben azt is nyertük, hogy a körök érintkezési pontja a beírt kör középpontját adja.
 

Megjegyzés. A versenyzők legnagyobb része csak a feladat egyik felét bizonyította be, mert nem volt tisztában azzal, hogy az >>akkor és csakis akkor<< azt jelenti, hogy be kell bizonyítani egyrészt, hogy a feltétel elégséges (>>akkor<<) és másrészt, hogy a feltétel egyszersmind szükséges is (>>csakis akkor<<), vagyis azt, hogy a tétel megfordítható. Hogy ez nincs mindig így ‐ tehát bizonyításra szorul ‐ ezt a következő két igen egyszerű példa világítja meg. >>Ha egy szám 5-re végződik, akkor osztható 5-tel. Itt az >>akkor<< nem toldható meg >>csakis akkor<<-ral, mert az 5-re végződés elégséges feltétel ugyan, de nem szükséges, hiszen a 0-ra végződő számok is oszthatók 5-tel. Viszont a következű állításban: >>Egy szám csakis akkor osztható 6-tal, ha páros<<, nem írhatunk a >>csakis akkor<< elé >>akkor<<-t, mert a szám páros volta ugyan szükséges feltétel, de nem elégséges, mert hiszen sok páros szám nem osztható 6-tal. Tehát a fenti két állítás egyike sem fordítható meg. (Ugyanis nem mondhatjuk: >>Az 5-re, végződő számok oszthatók 5-tel és fordítva, ha egy-egy szám osztható 5-tel, akkor 5-re végződik.<< Hasonlóképpen hamis: >>Minden 6-tal osztható szám páros és fordítva, minden páros szám osztható 6-tal.<<)