Kezdőlap


Feladat:	1992. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kós Géza
Füzet:	1993/január, 5 - 6. oldal		PDF \| MathML
Témakör(ök):	Teljes indukció módszere, Cauchy-Schwarz-Bunyakovszkij-féle egyenlőtlenség, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1992/október: 1992. évi Nemzetközi Matematika Diákolimpia 22. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az állítást a pontok száma szerinti teljes indukcióval fogjuk bizonyítani.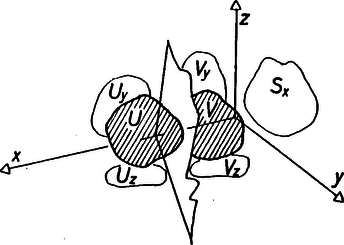
Először is megjegyezzük, hogy ha $a$ , $b$ , $c$ pozitív egészek és $S$ azokból a rácspontokból áll, amelyeknek $x$ koordinátája $1$ és $a$ , $y$ koordinátája $1$ és $b$ , $z$ koordinátája pedig $1$ és $c$ közé eső egész szám, akkor (1)-ben egyenlőség van, mert $| S | = a b c$ , $| S_{x} | = b c$ , $| S_{y} | = a c$ és $| S_{z} | = a b$ .
Ezért az indukciós lépésnél $S$ -nek csak olyan részhalmazait érdemes vizsgálni, amelyeket úgy kapunk, hogy $S$ -et egy, valamelyik koordinátasíkkal párhuzamos síkkal két részre vágjuk.
Ha csak egy pont van, akkor $| S | = | S_{x} | = | S_{y} | = | S_{z} | = 1$ , és az állítás igaz.
Tegyük most fel, hogy a pontok száma $| S | = n > 1$ , és $n$ -nél kevesebb pontra az állítás igaz.

Először megmutatjuk, hogy van olyan sík, amely valamelyik koordinátasíkkal párhuzamos és két nem üres részre osztja

S

-et. Ha

S

-et nem lehet egy, az

x

-tengelyre merőleges síkkal kettévágni, akkor

S

minden pontjának ugyanaz az

x

-koordinátája. Hasonlóan, ha az

y

- és a

z

-tengelyre merőlegesen sem lehet két nem üres részre kettévágni, akkor a pontoknak az

y

- és

z

- koordinátája is megegyezik. Mivel azonban

S

-nek legalább 2 pontja van, ez lehetetlen.
Mivel a feladatban a koordináta-tengelyek szerepe szimmetrikus, feltehetjük, hogy az

x

- tengelyre merőlegesen vágtuk szét

S

-et két nem üres részre.
Legyen a két rész

U

és

V

; pontjaiknak az

y z

x z

x y

-síkokra való ortogonális vetületeiből álló halmazok

U_{x}

U_{y}

U_{z}

, illetve

V_{x}

V_{y}

V_{z}

.
Az

U

és

V

halmazok konstrukciójából következik, hogy

\begin{matrix} | U | + | V | = | S |, | U_{y} | + | V_{y} | = | S_{y} |, | U_{z} | + | V_{z} | = | S_{z} |, \\ | U_{x} | \leq | S_{x} | és | V_{x} | \leq | S_{x} | . \end{matrix}

Ezen kívül, mivel

U

-nak és

V

-nek

n

-nél kevesebb pontja van, az indukciós feltevés szerint

\begin{matrix} | U |^{2} \leq | U_{x} | | U_{y} | | U_{z} | és | V |^{2} \leq | V_{x} | | V_{y} | | V_{z} | . \end{matrix}

Mindezek és a Cauchy ‐ Bunyakovszkij ‐Schwarz egyenlőtlenség felhasználásával

\begin{matrix} | S_{x} | | S_{y} | | S_{z} | = \\ = | S_{x} | (| U_{y} | + | V_{y} |) (| U_{z} | + | V_{z} |) = | S_{x} | ({\sqrt[]{| U_{y} |}}^{2} + {\sqrt[]{| V_{y} |}}^{2}) ({\sqrt[]{| U_{z} |}}^{2} + {\sqrt[]{| V_{z} |}}^{2}) ⩾ \\ ⩾ | S_{x} | {(\sqrt[]{| U_{y} |} \sqrt[]{| U_{z} |} + \sqrt[]{| V_{y} |} \sqrt[]{| V_{z} |})}^{2} = \\ = {(\sqrt[]{| S_{x} |} \sqrt[]{| U_{y} |} \sqrt[]{| U_{z} |} + \sqrt[]{| S_{x} |} \sqrt[]{| V_{y} |} \sqrt[]{| V_{z} |})}^{2} ⩾ \\ ⩾ {(\sqrt[]{| U_{x} | | U_{y} | | U_{z} |} + \sqrt[]{| V_{x} | | V_{y} | | V_{z} |})}^{2} ⩾ {(| U | + | V |)}^{2} = | S |^{2} . \end{matrix}

Ezzel az állítást igazoltuk.