| Feladat: | 1992. évi Nemzetközi Matematika Diákolimpia 21. feladata | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Kós Géza | ||
| Füzet: | 1993/január, 4 - 5. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Beírt kör, Hozzáírt körök, Középpontos és egyéb hasonlósági transzformációk, Egyenes, Nemzetközi Matematikai Diákolimpia | ||
| Hivatkozás(ok): | Feladatok: 1992/október: 1992. évi Nemzetközi Matematika Diákolimpia 21. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen a kör -ből induló átmérőjének másik végpontja , és -nek az -beli érintője . Egy tetszőleges ponthoz pontosan akkor léteznek -en olyan pontok, amelyekre a háromszög beírt köre, ha -nek az -et tartalmazóval ellentétes partjára esik. 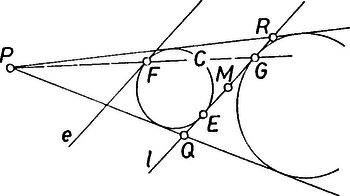 Legyen tetszőleges pont -nek az -lel ellentétes partján. A -ből -hez húzott érintők és metszéspontjai legyenek és . Azt kellene megállapítanunk, hogy milyen esetén felezőpontja -nek. Legyen az és a egyenesek metszéspontja. Nagyítsuk fel -ből -t úgy, hogy képe , azaz képe legyen. Mivel képe is érinti a és egyeneseket, valamint -et a -vel ellentétes oldalán, képe éppen a háromszögnek a oldalhoz hozzáírt köre. Ismeretes, hogy ha egy háromszög oldalai , és , félkerülete , akkor a beírt kör érintési pontja a oldalt úgy osztja ketté, hogy az oldal melletti szakasz hossza , a oldal melletti szakasz hossza , a oldalhoz hozzáírt kör érintési pontja pedig úgy osztja ketté, hogy az oldal melletti szakasz hossza , a oldal melletti szakasz hossza . Ebből következik, hogy (és ). Ezért pontosan akkor felezőpontja -nek, ha -nek is felezőpontja. A megfelelő pontok halmazát tehát a következőképpen kaphatjuk meg: Legyen az pont tükörképe -re. A keresett halmaz a szakasznak az -en túli meghosszabbítása, egy nyílt félegyenes. |