| Feladat: | 1992. évi Nemzetközi Matematika Diákolimpia 13. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Kós Géza | ||
| Füzet: | 1993/január, 3 - 4. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gráfok komplementere, Nemzetközi Matematikai Diákolimpia | ||
| Hivatkozás(ok): | Feladatok: 1992/október: 1992. évi Nemzetközi Matematika Diákolimpia 13. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A feladat valójában egy gráfelméleti kérdés, amely így fogalmazható át: Mekkora az a legkisebb , amelyre teljesül, hogy ha egy 9 pontú gráfnak éle van, akkor azokat akárhogyan színezzük ki pirosra vagy kékre, a gráf mindig tartalmazni fog egyszínű háromszöget? 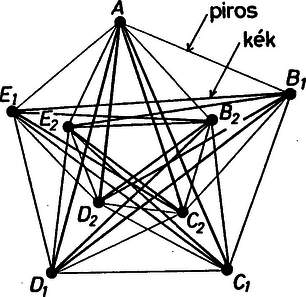 1. ábra Ha a gráfból legfeljebb él hiányzik, akkor válasszuk ki mindegyik hiányzó élnek valamelyik végpontját, és ezt a legfeljebb kiválasztott pontot hagyjuk el a gráfból. Ezzel az eredetinek egy olyan részgráfját kapjuk, amelynek legalább pontja van és amelyben már nincsenek hiányzó élek (vagyis a részgráf teljes). Az előbb idézett tétel szerint tehát a részgráf tartalmaz egyszínű háromszöget. A háromszög viszont az eredeti gráfnak is része. Ezzel igazoltuk, hogy ha a gráfnak legalább éle van, akkor tartalmaz egyszínű háromszöget. Most mutatunk egy pontú, élű gráfot, amelynek éleit ki lehet színezni két színnel úgy, hogy ne tartalmazzon egyszínű háromszöget (1. ábra). Megjegyezzük, hogy a négy hiányzó él közül semelyik kettőnek nem lehet közös végpontja, mert ellenkező esetben el lehetne hagyni három pontot (az egyiket a két él közös végpontjának választva) úgy, hogy a megmaradó 6 pontú gráf teljes legyen, az pedig biztosan tartalmaz egyszínű háromszöget. Ez a feltétel máris meghatározza, hogy mi a gráf; nekünk csak a színezést kell előírnunk. 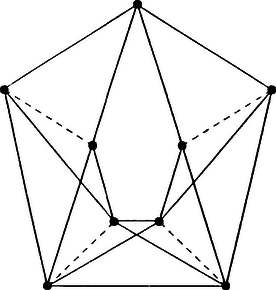 2. ábra A jobb áttekinthetőség érdekében folytonos szakaszokkal ábrázoljuk a piros éleket, a kék színűeket nem rajzoljuk be. A teljes gráfból kimaradó élet szaggatott vonal jelzi. A 2. ábráról jól látszik, hogy a gráf sem teljes háromszöget, sem pedig üres háromszöget nem tartalmaz. Megjegyzés. A felhasznált segédtétel a következőképpen bizonyítható be. Legyen a gráf egy tetszőleges pontja. Mivel -ból legalább él indul ki, az élek között van három egyszínű, mondjuk piros. Legyen ezek végpontja , és . Ha a , , pontok közül kettőt piros él köt össze, akkor ez a két pont -val együtt egy piros háromszöget alkot. Ha pedig a háromszög élei közül egyik sem piros, akkor egy kék háromszög. |