Kezdőlap


Feladat:	1991. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kőszegi Botond
Füzet:	1991/november, 340 - 341. oldal		PDF \| MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Számtani-mértani egyenlőtlenségek, Jensen-féle egyenlőtlenség, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1991/szeptember: 1991. évi Nemzetközi Matematika Diákolimpia 22. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Használjuk az ábra jelöléseit.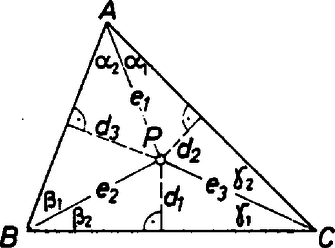

Vegyük észre, hogy

\begin{matrix} \frac{sin α_{1} sin β_{1} sin γ_{1}}{sin α_{2} sin β_{2} sin γ_{2}} = \frac{\frac{d_{2}}{e_{1}} \cdot \frac{d_{3}}{e_{2}} \cdot \frac{d_{1}}{e_{3}}}{\frac{d_{3}}{e_{1}} \cdot \frac{d_{1}}{e_{2}} \cdot \frac{d_{2}}{e_{3}}} = 1. \end{matrix}

Tegyük fel, hogy a feladat állítása nem igaz, tehát

α_{1}, β_{1},

és

γ_{1}

is nagyobb, mint

30^{\circ}

. Ha például

α \geq 150^{\circ}, β

és

γ

is kisebb, mint

30^{\circ}

, így máris ellentmondásra jutottunk. Ha pedig

α, β

és

γ

mindegyike kisebb

150^{\circ}

-nál, akkor

sin α \cdot sin β \cdot sin γ > \frac{1}{8}

. Ugyanakkor a számtani és a mértani közepek közti egyenlőtlenség szerint

\begin{matrix} sin α_{2} sin β_{2} sin γ_{2} \leq {(\frac{sin α_{2} + sin β_{2} + sin γ_{2}}{3})}^{3} . \end{matrix}

A Jensen-egyenlőtlenséget felhasználva (hisz a

sin

függvény a

[0, π]

intervallumon konkáv)

\begin{matrix} sin α_{2} + sin β_{2} + sin γ_{2} \leq 3 sin \frac{α_{2} + β_{2} + γ_{2}}{3} . \end{matrix}

De mivel

0^{\circ} < α_{2} + β_{2} + γ_{2} < 90^{\circ}, 3 sin \frac{α_{2} + β_{2} + γ_{2}}{3} < \frac{3}{2}

, így

\begin{matrix} sin α_{2} sin β_{2} sin γ_{2} < {(\frac{\frac{3}{2}}{3})}^{3} = \frac{1}{8}, \end{matrix}

vagyis

\begin{matrix} \frac{sin α_{1} sin β_{1} sin γ_{1}}{sin α_{2} sin β_{2} sin γ_{2}} > 1. \end{matrix}

Ezzel ellentmondásra jutottunk, tehát bizonyítottuk a feladat állítását.