Feladat: 1989. évi Nemzetközi Matematika Diákolimpia 21. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Benczúr Péter 
Füzet: 1989/november, 351 - 353. oldal  PDF  |  MathML 
Témakör(ök): Síkgeometriai számítások trigonometria nélkül négyszögekben, Hiperbola egyenlete, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1989/szeptember: 1989. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A 2. napon az első nap már elég jól bevált taktikát akartam követni, vagyis a geometria feladattal kezdeni. Az első sikertelen másfél óra után váltottam csak az 5. feladatra. Azt megoldva tértem vissza a 4.-re, és ez "be is jött''.
Az első nehézséget maga az állítás okozta. Mit kezdjek szakaszok négyzetgyökeinek reciprokával? Könnyebben értelmezhetőnek tűnt ehelyett a AD⋅BC≧h⋅AD+h⋅BC állítást igazolni. Ezeknek a következő geometriai jelentést tulajdoníthatjuk: könnyen ellenőrizhető, hogy 2xy nem más, mint x és y sugarú egymást kívülről érintő körök közös érintőszakasza.
A következő részcél ilyen körök keresése a négyszögben. Itt sikerült hasznosítanom az első másfél órám eredményeit is. Ez az idő a következő ötletre "ment rá''. Rögzítsük AD, BC hosszát, változtassuk h hosszát, majd egy-egy ((AD;BC;h) hármashoz próbáljunk ABCD négyszög(ek)et szerkeszteni.
Mivel AB=AD+BC; AP=AD+h; BP=BC+h, ezért ekkor az ABP háromszög megszerkeszthető. A C pont mértani helye a B körüli, BC sugarú kB kör, a D ponté a hasonló kA kör. A CD szakasz pedig érinti a P körüli, h sugarú kP kört. Megvan a három kör! Annak a feltétele, hogy létrejöjjön legalább egy ,,jó'' ABCD négyszög, az, hogy legyen a kP körnek olyan érintője, amelynek van közös pontja a kA és kB körökkel is, méghozzá úgy, hogy a metszéspontok az AB egyenes P felőli partján legyenek, (hogy a négyszög konvex legyen). Ehhez az nyilván elégséges, hogy kP teljesen az AB felőli partján legyen kA és kB közös külső érintőinek; legfeljebb érintse. De ez szükséges is, mert ellenkező esetben a következő igaz: a kA és kB bármely X, illetve Y pontját összekötve, ez a szakasz a közös érintő alatt AB felé eső részén) halad, így kP-t csak oly módon érintheti, ha P a létrejövő XYAB négyszög külső pontja.

 
 
1. ábra
 

Az volt az elképzelésem, hogy igazolom a AD⋅BC≧(AD+BC)h helyességét. Látható, hogy h változtatásával a bal oldal állandó, a jobb oldal pedig ugyanolyan irányban változik. Ha belátnánk, hogy h maximumakor egyenlőség áll fenn, akkor készen lennénk. Az 1. ábrát tanulmányozva észrevehetjük, hogy ha kP érinti kA és kB közös érintőjét, akkor RQ=2⋅AD⋅h; QZ=2⋅BC⋅h; RZ=2⋅AD⋅BC, és RQ+QZ=RZ. Azaz itt egyenlőség áll fenn. Vonzónak tűnik belátni, hogy h erre az esetre maximális. Ekkor már az egyenlőség feltétele is megvan: az ABCD derékszögű trapéz (ADC∢=DCB∢=90∘). Ezt nem túl elegáns úton sikerült befejeznem. Találhattam volna szebb módot is, de az elkövetkezőkben felhasznált részeredményeim már hamarabb elkészültek, így ez tűnt a leggyorsabb útnak.
Legyen koordinátarendszerünk középpontja az A pont, A(0;0); legyen AD=s, BC=z és feltehető, hogy BC≧AD. Mivel BP-AP=BC-AD= konstans, ezért h változtatásával P egy fél hiperbola ágon mozoghat (2. ábra). Ezen látszik, hogy ha x csökken, az y nő (ez az egyenessé torzult hiperbolánál (AD=BC) is elfogadható).  Belátjuk, hogy h növelésével x csökken (vagy állandó marad, az egyenes esetén ), azaz y nő. Így egyre feljebb kerül kP azon S pontja, amelyre SP⊥AB és S a P fölött van. Ez a pont tehát egyre feljebb kerül, de az érintőnél levő helyzetnél nem mehet tovább. Így valóban az érintőnél lesz h maximális.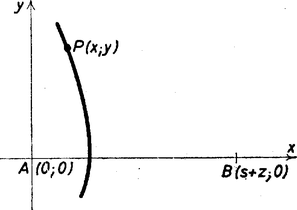
 
 
2. ábra
 

Ugyanakkor a P(x;y) pontra AP=s+h azaz
(1) x2+y2=(s+h)2; BP=z+h, azaz
(2) (s+z-x)2+y2=(z+h)2;
ezek különbségéből
 

x=(s+z)+(s-z)(s+z+2h)2(s+z).
 


Ez egy elsőfokú függvénye h-nak, és az együtthatója s-z2(s+z)≦0; azaz h növelésével y is nő. Vagyis állításunkat beláttuk.