Kezdőlap


Feladat:	1989. évi Nemzetközi Matematika Diákolimpia 12. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Pásztor Gábor
Füzet:	1989/november, 349 - 350. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Szögfelező egyenes, Hozzáírt körök, Feuerbach-kör, Középponti és kerületi szögek, Terület, felszín, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1989/szeptember: 1989. évi Nemzetközi Matematika Diákolimpia 12. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a háromszög egy szögének külső és belső szögfelezője merőleges egymásra, az $A, B, C$ pontok az $A_{0} B_{0} C_{0}$ háromszögben a magasságvonalak talppontjai. Ismeretes, hogy egy háromszög Feuerbach-köre áthalad a magasságok talppontjain, az $A B C$ háromszög köré írt köre tehát az $A_{0} B_{0} C_{0}$ háromszög Feuerbach-köre. A Feuerbach-kör áthalad az $O A_{0}, O B_{0}, O C_{0}$ felezőpontján is, ezért $O A_{1} = A_{1} A_{0}$ , $O B_{1} = B_{1} B_{0}$ , $O C_{1} = C_{1} C_{0}$ .

3. ábra

Jelöljük a kis háromszögek területét

t_{i}

-vel

(i = 1,2, ... 12)

az ábra szerint. Így

t_{1} = t_{7}

, mert a két háromszög alapja és magassága egyenlő. Ugyanígy kapjuk, hogy

t_{2} = t_{8}

t_{3} = t_{9}

t_{4} = t_{10}

t_{5} = t_{11}

t_{6} = t_{12}

. Ezeket összeadva:

\begin{matrix} t_{1} + t_{2} + ... + t_{6} = t_{7} + t_{8} + ... + t_{12} . \end{matrix}

Mindkét oldalhoz hozzáadva az egyenlet bal oldalát:

\begin{matrix} 2 (t_{1} + t_{2} + ... + t_{6}) = t_{1} + t_{2} + ... + t_{12} \end{matrix}

ami éppen a bizonyítandó állítás.

A második állítás igazolásához ezután elegendő belátni, hogy az

A C_{1} B A_{1} C B_{1}

hatszög területe legalább kétszerese az

A B C

háromszög területének.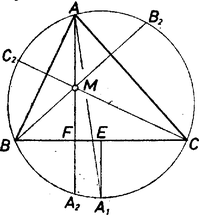

4. ábra

Jelöljük az

A B C

háromszög magasságpontjának az oldalakra vonatkoztatott tükörképeit rendre

A_{2}, B_{2}, C_{2}

-vel. Ismert, hogy ezek a pontok a körülírt körön vannak. Az

A_{1}

pont a

B C

ív (

A

-t nem tartalmazó ívének) felezőpontja, mert

B A_{1}

és

C A_{1}

ívekhez tartozó kerületi szögek egyenlők, tehát az

A_{1} E

szakasz (

E

B C

szakasz felezőpontja) nem kisebb az

A_{2} F

szakasznál (

F

A_{2}

vetülete

B C

-re).
Ezért

t_{B A_{1} C} ≧ t_{B A_{2} C}

. Hasonlóan kapjuk, hogy

t_{C B_{1} A} ≧ t_{C B_{2} A}

t_{A C_{1} B} ≧ t_{A C_{2} B}

. Az egyenlőtlenségek megfelelő oldalait összeadva

\begin{matrix} t_{B A_{1} C} + t_{C B_{1} A} + t_{A C_{1} B} ≧ t_{B A_{2} C} + t_{C B_{2} A} + t_{A C_{2} B} . \end{matrix}

A jobb oldalon éppen az

A B C

háromszög területe áll, mert a kis háromszögeket tükrözve az oldalegyenesekre

A_{2}

B_{2}

C_{2}

pontok tükörképe éppen a magasságpont, és így a tükörképek egyrétűen fedik le az

A B C

háromszöget.
Azaz

\begin{matrix} t_{B A_{1} C} + t_{C B_{1} A} + t_{A C_{1} B} ≧ t_{A B C} . \end{matrix}

Mindkét oldalhoz hozzáadva

t_{A B C}

-t

\begin{matrix} t_{A B C} + t_{B A_{1} C} + t_{C B_{1} A} + t_{A C_{1} B} ≧ 2 t_{A B C} . \end{matrix}

Így éppen a bizonyítandó állítást kapjuk, mert a bal oldal

4

háromszöge éppen lefedi az

A C_{1} B A_{1} C B_{1}

hatszöget.
Egyenlőség csak akkor állhat fenn, ha

A_{1}

és

A_{2}

B_{1}

és

B_{2}

C_{1}

és

C_{2}

egybeesik, ami azt jelenti, hogy a háromszög minden alapról nézve egyenlő szárú, tehát szabályos. Szabályos háromszögben pedig nyilván fennáll az egyenlőség.