Feladat: 1989. évi Nemzetközi Matematika Diákolimpia 11. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Pásztor Gábor 
Füzet: 1989/november, 348 - 349. oldal  PDF  |  MathML 
Témakör(ök): Konstruktív megoldási módszer, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1989/szeptember: 1989. évi Nemzetközi Matematika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az ilyen típusú feladatokra általában kétféle megoldás lehetséges. Az egyik csak a felosztás létezését igazolja, a másik megkonstruálja a felosztást is. Én ez utóbbit választottam. Sikerült találnom egy olyan módszert, amely két lépésben elkészíti a kívánt felosztást. Könnyen ellenőrizhető, hogy 1989=17⋅117. Ezt felhasználva első lépésben soroljuk be a számokat az ábrán látható módon.

 
 
1. ábra
 

Minden sorban pontosan 17 szám van, ezek alkotnak egy csoportot. Az első sorban a számok összege éppen megfelelő. Maradt 116 sorunk. Vizsgáljuk meg ezeket párosával az ábra szerint. Az A és C-vel jelzett csoportokban az egy sorban lévő számok összege mindenütt 995⋅16, tehát ugyanannyi. Csak a B-vel jelzett részben a "középső'' satírozott elem változik. Minden egyes párban a B-ben lévő elem ugyanannyival tér el a 995-től, az egyikük nagyobb, a másikuk kisebb. Tehát két ilyen szomszédos sorban is megfelelő a számok együttes összege. Ha a szomszédos sorokat párosával rendbe tudjuk tenni, akkor készen is vagyunk.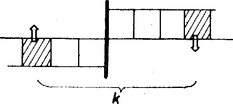
 
 
2. ábra
 

Második lépésben tehát vegyük azt a párt, ahol a középső B-beli elemnek a 995-től való eltérése éppen d. (d 1-től 58-ig változhat, mert 2⋅58+1=117). A pár első sorában a kívánt értéktől való eltérés d, a másodikban ‐ d. Ha a C-beli nyolcasokban kicserélünk az ábrán látható módon két számot, melyek egymástól k távolságra vannak (1≦k≦15), akkor az egyik sorban k-val nő, a másikban pedig k-val csökken az összeg. Ha 1≦d≦15, akkor így egyetlen cserével helyrehozható az eltérés. Ha az eltérés nagyobb 15-nél, akkor a két szélsőt kicseréljük, és a maradék 14 számmal tetszőlegesen megmaradó különbség helyrehozható 1-től 13-ig. Ha még ez sem elég, akkor a 14 szám közül a két szélsőt ismét cseréljük ki. A maradék 12 számmal tetszőlegesen megmaradó különbség korrigálható 1-től 11-ig. Látható, hogy C-beli elemek alkalmas cseréjével tetszőleges eltérés korrigálható az alábbi határig:15+13+11+...+3+1=64. Ez nagyobb mint 58, tehát mindegyik párnál elvégezhető a csere. Ezzel a feladatot megoldottuk.