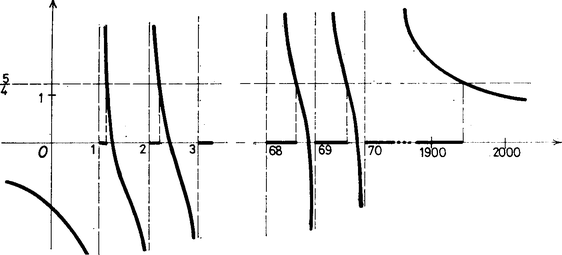Feladat: 1988. évi Nemzetközi Matematika Diákolimpia 21. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Drasny Gábor 
Füzet: 1988/október, 293 - 295. oldal  PDF  |  MathML 
Témakör(ök): Függvény határértéke, Függvények folytonossága, Gyökök és együtthatók közötti összefüggések, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1988/szeptember: 1988. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Vezessük be a következő jelöléseket:

f(x)=∑k=170kx-k;I0=(-∞,1),I1=(1,2),I2=(2,3),......,Ii(i,i+1),...,I69=(69,70),I70=(70,+∞).


Az f(x) értelmezési tartománya I0∪I1∪...∪I70, mivel f(x) az 1,2,3,...,70 értékek kivételével nyilván mindenütt értelmes. f(x) az értelmezési tartományában folytonos, mert folytonos függvények összegeként áll elő.
 
 

Az egyes intervallumokban f(x) szigorúan monoton csökken, hiszen szigorúan monoton csökkenő függvények (1x-1,2x-2,...,70x-70) összegeként áll elő.
I0-ban a függvény csak negatív értékeket vesz fel, az 1x-1,2x-2,...,70x-70 törtek mindegyike negatív ebben az intervallumban.
Az I1,I2,...,I69 intervallumban f(x) minden valós értéket felvesz, az egyes intervallumokon belül f(x) folytonos, másrészt, mint azt látni fogjuk, az intervallumok bal oldalán f(x) jobb oldali határértéke +∞; az intervallumok jobb oldalán f(x) bal oldali határértéke -∞. Ezt a következő módon láthatjuk be: legyen "a'' az 1, 2, 3, ..., 70 egészek bármelyike. Ekkor
limx→a+0f(x)=limx→a+0∑k=170kx-k=∑k=170limx→a+0kx-k=+∞,


k=a esetén
limx→a+0kx-k=limx→a+0ax-a=+∞,


minden más esetben limx→a+0kx-k véges. Hasonlóképpen igaz, hogy limx→a-0f(x)=-∞.
Már láttuk, hogy f(x)-nek az x=70 helyen vett jobb oldali határértéke +∞. Másrészt igaz az is, hogy limx→+∞f(x)=0, hiszen limx→+∞f(x)=∑k=170limx→+∞kx-k=∑k=1700=0. Így az I70 intervallumban a függvény minden pozitív értéket felvesz.
A függvény menete tehát a következő (vázlatosan):
Az f(x)=54 egyenletnek tehát az I0 intervallum kivételével mindegyik intervallumban van megoldása, a szigorú monotonitás miatt minden intervallumban pontosan egy. A gyökök legyenek rendre x1,x2,...,x70. Ekkor 1<x1<2<x2<3<...<70<x70.
Az f(x)≧54 egyenlőtlenség megoldáshalmaza ekkor nyilván az (1,x1]∪(2,x2]∪...∪(70,x0] halmaz. Ezek valóban diszjunkt intervallumok, összhosszuk:
S=(x1-1)+(x2-2)+...+(x70-70)=(x1+x2+...+x70)-(1+2+...+70)


Hozzuk közös nevezőre a
-54+f(x)=1x-1+2x-2+...+70x-70-54


összeget.
-54+f(x)=1⋅(x-2)(x-3)...(x-70)+2⋅(x-1)(x-3)⋅...⋅(x-70)(x-1)(x-2)⋅...⋅(x-70)++...+70(x-1)(x-2)⋅...⋅(x-69)(x-1)(x-2)⋅...⋅(x-70)-54(x-1)(x-2)⋅...⋅(x-70)(x-1)(x-2)⋅...⋅(x-70);


(A két sor egyetlen törtnek tekintendő.) A számláló egy 70-ed fokú polinom, főegyütthatója a70=-54. A 69-ed fokú tag együtthatója:
a69=1+2+...+70+54(1+2+...+70)=94(1+2+...+70).



Másrészt az f(x)=54 egyenlőség akkor és csak akkor teljesül, ha az f(x)-54 tört számlálója 0, így az x1,x2,...,x70 gyökök megegyeznek a fenti tört számlálójában szereplő polinom gyökeivel, így összegük is megegyezik. A Vieta-formula *szerint

x1+x2+...+x70=-a69a70=-94(1+2+...70)-54=95(1+2+...70).


Az intervallumok összhossza tehát:
S=95(1+2+...+70)-(1+2+...+70)=45(1+2+...+70)==45⋅71⋅70⋅12=2⋅71⋅14=1988,


és ezt kellett bizonyítani.
Drasny Gábor (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)
*Legyen az f(x)=xn+a1xn-1+...+an komplex együtthatós polinom gyöktényezős alakja
f(x)=(x-α1)(x-α2)⋅...⋅(x-αn);
az együtthatók összehasonlítása alapján adódó összefüggések:
α1+α2+...+αn=-a1,α1α2+α1α3...+α1αn+α2α3+...+αn-1αn=a2,⋮α1α2...αn=(-1)nan.



Ezeket nevezzük Viéta-formuláknak.