Kezdőlap


Feladat:	1986. évi Nemzetközi Matematika Diákolimpia 21. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Kós Géza
Füzet:	1986/november, 357 - 358. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszögek geometriája, Pont körüli forgatás, Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Szögfüggvények, síkgeometriai számítások, Húrnégyszögek, Szinusztétel alkalmazása, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1986/szeptember: 1986. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

4. feladat. Legyenek $A$ és $B$ egy $O$ középpontú szabályos $n$ -szög $(n \geq 5)$ szomszédos csúcsai. Egy, az $O A B$ háromszöggel egybevágó $X Y Z$ háromszöggel először befedjük $O A B$ -t, majd az $X$ pontot úgy mozgatjuk ‐ mindig az $n$ -szög belsejében ‐, hogy eközben az $Y$ és $Z$ pontok állandóan az $n$ -szög oldalain legyenek. Milyen alakzatot ír le $X$ , ha $Y$ befutja az $n$ -szög határát (kerületét)?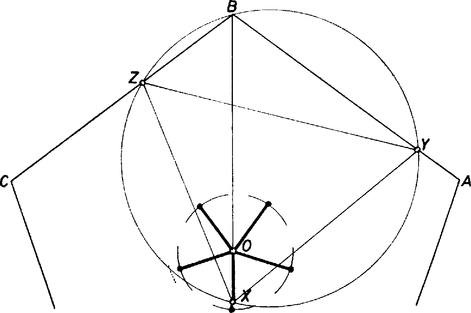

Megoldás. Állítjuk, hogy a keresett ponthalmaz

n

darab zárt szakaszból áll, amelyek hossza

O B (\frac{1}{cos \frac{π}{n}} - 1)

, és amelyek az

n

-szög csúcsait

O

-val összekötő szakaszok

O

-n túli meghosszabbításai.
Ha

Y

és

Z

két szomszédos csúccsal esik egybe, akkor

X \equiv O

; a többi esetben

X

két szomszédos oldal által határolt kisebbik szögtartományban helyezkedik el (ennek igazolásától most eltekintünk).
Legyen most

Y

A B

Z

pedig a vele szomszédos

B C

oldal belső pontja. Ekkor

Y B Z ∢ = A B C ∢ = π - \frac{2 π}{n}

Y X Z ∢ = \frac{2 π}{n}

, e két szög összege tehát

π

, vagyis az

X Y B Z

négyszög húrnégyszög. Mivel

X Y = X Z

X B Y

és

X B Z

szögekhez egyenlő ívek tartoznak, ezért

X B Y ∢ = X B Z ∢

; az

X

pont az

Y B Z ∢ = A B C ∢

szögfelezőjén helyezkedik el.
Vizsgáljuk most meg, mekkora lehet a

B Z

távolság! Először belátjuk, hogy

B X > O B

. Ugyanis

X Y B ∢ + X Z B ∢ = π

, így közülük az egyik legalább

\frac{π}{2}

, mondjuk

X Z B ∢ \geq \frac{π}{2}

. De

X B Z ∢ < \frac{π}{2}

, ezért az

X Z B

háromszögben ezen szögekkel szemben fekvő oldalakra

B X > X Z

adódik

X Z B ∢ > X B Z ∢

miatt. És itt

X Z = O B

. Másodszor

B X

szakasz hosszára felső becslés az

X Y B Z

húrnégyszög köré írható kör átmérője. Ez pedig a szinusztétel segítségével

\begin{matrix} \frac{Y Z}{sin Y X Z ∢} = \frac{O B}{sin (\frac{π}{2} - \frac{π}{n})} = \frac{O B}{cos \frac{π}{n}} . \end{matrix}

Ehhez hozzávéve a megoldás elején említett

X \equiv A

Y \equiv B

Z \equiv O

esetet,

\begin{matrix} 0 \leq O X \leq \frac{O B}{cos \frac{π}{n}} - O B = O B (\frac{1}{cos \frac{π}{n}} - 1) \end{matrix}

adódik. Ha pedig gondolatmenetünket elvégezzük a többi szomszédos oldalpárra is, akkor kiderül, hogy

X

csakis a megoldás elején leírt ponthalmaz pontja lehet.
Hátravan még annak igazolása, hogy az említett halmaz minden pontja megfelelő. Legyen

X'

B O

félegyenesen úgy, hogy

O B < B X' \leq \frac{O B}{cos \frac{π}{n}}

. Rajzoljuk meg a

B

-n és

X'

-n átmenő,

\frac{O B}{cos \frac{π}{n}}

átmérőjű körök valamelyikét (ha

B X' = \frac{O B}{cos \frac{π}{n}}

, akkor csak egy ilyen van). Az olvasóra bízzuk annak igazolását, hogy ez a kör metszi az

A B

és

B C

szakaszokat. Jelöljük ezen metszéspontokat

Y'

-vel és

Z'

-vel. Mivel

Y' B X' ∢ = X' B Z' ∢

, azért

X' Y' = X' Z'

. Másrészt mivel

X' Y' B Z'

négyszög húrnégyszög,

Y' X' Z' ∢ = π - Y' B Z' ∢ = \frac{2 π}{n}

. Ezért az

X' Y' Z'

háromszög hasonló az

A B O

háromszöghöz, körülírt köreik pedig ugyanakkorák, ezért a két háromszög egybevágó. Ez a meggondolás bizonyítja, hogy a megadott ponthalmaz minden pontja jó.