Kezdőlap


Feladat:	1982. évi Nemzetközi Matematika Diákolimpia 12. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Csirmaz László , Megyesi Gábor
Füzet:	1984/január, 8 - 9. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Beírt kör, Hozzáírt körök, Feuerbach-kör, Inverzió, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1982/szeptember: 1982. évi Nemzetközi Matematika Diákolimpia 12. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az a feltétel, hogy a $A_{1} A_{2} A_{3}$ háromszög nem egyenlő szárú, biztosítja, hogy a kérdéses egyenesek léteznek és különbözők. Tükrözzük a háromszög $a_{1}$ oldalegyenesét az $A_{1}$ csúcsból induló belső szögfelezőre. A kapott $b_{1}$ egyenes érinti a $k$ beírt kört, mégpedig $T_{1}$ pont tükörképében, azaz $S_{1}$ -ben, továbbá érinti a háromszög $a_{1}$ -hez hozzáírt $k_{1}$ körét is (1. ábra).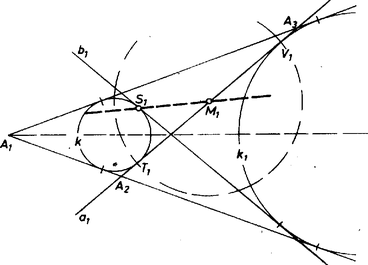

1. ábra

Tekintsük az

M_{1}

középpontú,

M_{1} T_{1} = M_{1} V_{1}

sugarú körre vonatkozó inverziót. Ez az inverzió helyben hagyja a

k

és

k_{1}

köröket, hiszen mindkettő merőleges az inverzió alapkörére: a

T_{1}

, illetve

V_{1}

metszéspontokból a középpontokba mutató sugarak merőlegesek egymásra. Állítjuk, hogy a

b_{1}

egyenes inverze éppen a háromszög Feuerbach-köre. Ebből a feladat állítása következik. Mivel

b_{1}

érinti

k

-t és

k_{1}

-et is, azért

b_{1}

inverze érinti

k

-nak, valamint

k_{1}

-nek inverzét, következésképp egy háromszög Feuerbach-köre érinti a háromszög beírt körét, továbbá a három hozzáírt kört is.
A beírt kör és a Feuerbach-kör érintési pontja inverz képe annak a pontnak, ahol

b_{1}

és

k

érinti egymást, vagyis az

S_{1}

pontnak, és így rajta van az

M_{1} S_{1}

egyenesen. Ugyanez az érintési pont rajta van az

M_{2} S_{2}

M_{3} S_{3}

egyeneseken is, s így

M_{1} S_{1}

M_{2} S_{2}

M_{3} S_{3}

valóban egy ponton mennek át, ahogyan a feladat állította.
Annak igazolása maradt még hátra, hogy

b_{1}

inverz képe a háromszög Feuerbach-köre. Mivel

b_{1}

nem megy át az inverzió középpontján,

M_{1}

-en (

a_{2} \neq a_{3}

miatt),

b_{1}

inverze egy

M_{1}

-en átmenő kör. S mivel az

A_{1} A_{2} A_{3}

háromszög Feuerbach-köre az

M_{1} M_{2} M_{3}

középháromszög körülírt köre, elegendő megmutatnunk, hogy

M_{2}

és

M_{3}

is rajta van

b_{1}

inverz képén, azaz

\begin{matrix} M_{1} X \cdot M_{1} M_{2} = M_{1} Y \cdot M_{1} M_{3} = M_{1} T_{1}^{2}, \end{matrix}

ahol

X

, ill.

Y

M_{1} M_{2}

, ill.

M_{1} M_{3}

félegyenesnek és a

b_{1}

-nek metszéspontjai (2. ábra). Mivel

A_{2} T_{1} = s - a_{2} = (a_{1} + a_{3} - a_{2}) / 2

és

M_{1} A_{2} = a_{1} / 2

, azért

\begin{matrix} M_{1} T_{1}^{2} = {(M_{1} A_{2} - A_{2} T_{1})}^{2} = \frac{{(a_{2} - a_{3})}^{2}}{4} . \end{matrix}

P

A_{1}

-ből induló belső szögfelezőnek és

a_{1}

-nek a metszéspontja, tehát

\begin{matrix} P A_{2} = \frac{a_{1} a_{3}}{a_{2} + a_{3}}, P A_{3} = \frac{a_{1} a_{2}}{a_{2} + a_{3}}, \\ P M_{1} = | M_{1} A_{2} - P A_{2} | = \frac{a_{1} | a_{2} - a_{3} |}{2 (a_{2} + a_{3})} . \end{matrix}

2. ábra

Végül a

P X M_{1}

és

P Q A_{2}

hasonló háromszögekből

\begin{matrix} M_{1} X : A_{2} Q = P M_{1} : P A_{2} = \frac{a_{1} | a_{2} - a_{3} |}{2 (a_{2} + a_{3})} \cdot \frac{a_{2} + a_{3}}{a_{1} a_{3}} = \frac{| a_{2} - a_{3} |}{2 a_{3}}, \end{matrix}

vagyis

\begin{matrix} M_{1} X \cdot M_{1} M_{2} = \frac{| a_{2} - a_{3} |}{2 a_{3}} \cdot A_{2} Q \cdot M_{1} M_{2} = \frac{{(a_{2} - a_{3})}^{2}}{2 a_{3}} \cdot \frac{a_{3}}{2} = M_{1} T_{1}^{2} . \end{matrix}

P Y M_{1}

és

P R A_{3}

hasonló háromszögekből pedig

\begin{matrix} M_{1} Y : A_{3} R = P M_{1} : P A_{3} = \frac{| a_{2} - a_{3} |}{2 a_{2}}, \end{matrix}

vagyis

\begin{matrix} M_{1} Y \cdot M_{1} M_{3} = \frac{| a_{2} - a_{3} |}{2 a_{2}} \cdot | a_{2} - a_{3} | \cdot \frac{a_{2}}{2} = M_{1} T_{1}^{2} . \end{matrix}

Ezzel a feladat állítását beláttuk, s azt is, hogy ez a közös pont éppen a beírt kör és a Feuerbach-kör érintési pontja.