Kezdőlap


Feladat:	1979. évi Nemzetközi Matematika Diákolimpia 13. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Le Ba Khanh Trinh
Füzet:	1979/szeptember, 4 - 5. oldal		PDF \| MathML
Témakör(ök):	Forgatva nyújtás, Thalesz-kör, Trapézok, Derékszögű háromszögek geometriája, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1979/szeptember: 1979. évi Nemzetközi Matematika Diákolimpia 13. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a $k_{1}$ , ill. $k_{2}$ körök középpontját $O_{1}$ -gyel, ill. $O_{2}$ -vel, a két kör $A$ -tól különböző metszéspontja legyen $B$ . Először megmutatjuk, hogy a $P_{1}$ , $P_{2}$ , $B$ pontok a mozgás bármely pillanatában egy egyenesen vannak.
Ehhez figyeljük meg a következőket: ha az $A B_{1} C_{1}$ , $A B_{2} C_{2}$ $A B_{3} C_{3}$ , $...$ hasonló, és egyező körüljárású háromszögeknél a $B_{1}$ , $B_{2}$ , $B_{3}$ , $...$ pontok egy egyenesen vannak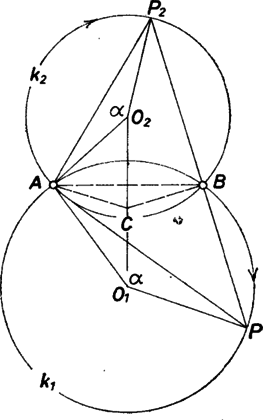, akkor a $C_{1}$ , $C_{2}$ , $C_{3}$ , $...$ pontok is egy egyenesen fekszenek. Ez egyszerűen következik abból, hogy a $B_{1}$ , $B_{2}$ , $B_{3}$ , $...$ pontokat az $A$ középpontú, $B_{1} A C_{1}$ szögű és $A C / A B$ arányú forgatvanyújtás viszi át rendre a $C_{1}$ , $C_{2}$ , $C_{3}$ , $...$ pontokba, és a forgatvanyújtás egyenestartó. Ez igaz abban az esetben is, ha a hasonló háromszögek helyett egy egyenesbe eső hasonló ponthármasokat mondunk.

1. ábra

A feladat feltétele szerint a

P_{1}

P_{2}

pontok a körök középpontjai körül állandó szögsebességgel forognak. Tegyük fel, hogy pl. a kiindulási

A

helyzettől

α

szöggel fordultak el

(0 < α < 2 π)

(1. ábra). Az

A O_{1} P_{1}

A O_{2} P_{2}

egyező körüljárású, hasonló, egyenlő szárú (esetleg elfajult) háromszögek. Mivel az

O_{1} O_{2}

egyenes az

A B

szakasz felező merőlegese, szerkeszthetünk rajta olyan

C

pontot, hogy az

A C B

és

A O_{1} P_{1}

háromszögek hasonlóak és egyező körüljárásúak legyenek. Előző megjegyzésünk értelmében így a

P_{1}

P_{2}

B

pontok valóban egy egyenesen vannak, mivel

O_{1}

O_{2}

C

is egy egyenesen fekszenek.
Elegendő most már azt bizonyítanunk, hogy a

P_{1} P_{2}

szakasz felező merőlegese ‐ a

P_{1} P_{2}

szakasz elhelyezkedésétől függetlenül ‐ átmegy egy rögzített ponton. Messe az

A B

-re

A

-ban állított merőleges a

k_{1}

, ill.

k_{2}

kört

X

-ben, ill.

Y

-ban, és legyen

X Y

felezőpontja

P

(2. ábra).

2. ábra

B X

és

B Y

szakaszok Thalész tétele szerint köreikben átmérők, ezért az

X P_{1} P_{2} ∢

és

Y P_{2} P_{1} ∢

derékszög, az

X P_{1} P_{2} Y

négyszög tehát derékszögű trapéz (hurkolt is lehet, és derékszögű háromszöggé is fajulhat). Következésképpen a

P_{1} P_{2}

szár felező merőlegese átmegy a rögzített

X Y

szár

P

felezési pontján; ezzel állításunkat igazoltuk.