Feladat:	1978. évi Nemzetközi Matematika Diákolimpia 21. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1978/október, 53. oldal		PDF  |  MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Beírt kör, Körök, Derékszögű háromszögek geometriája, Háromszögek hasonlósága, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1978/szeptember: 1978. évi Nemzetközi Matematika Diákolimpia 21. feladata

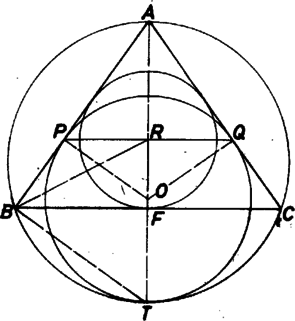
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   Jelöljük az érintő kör középpontját $O$-val, az érintési pontot $T$-vel, $BC$ felezőpontját $F$-fel és $PQ$ felezőpontját $R$-rel (l. ábra). Az ábra szimmetriája folytán az $A\mathrm{,}R\mathrm{,}O\mathrm{,}F\mathrm{,}T$ pontok mind rajta vannak a háromszög szimmetriatengelyén. $OP=OT$, hiszen mindkettő az érintő kör sugarával egyenlő, ezért a hasonló $APO$ és $ABT$ derékszögű háromszögekből $\begin{array}{c}{\displaystyle AP:PB=AO:OT=AO:OP=AP:PR\mathrm{,}}\end{array}$ hiszen $AOP$ és $APR$ is hasonló háromszögek. Így $PB=PR$, azaz $BPR$ egyenlő szárú háromszög, tehát $\begin{array}{c}{\displaystyle ABR\sphericalangle =PBR\sphericalangle =BRP\sphericalangle =RBC\sphericalangle \mathrm{,}}\end{array}$ mert utóbbi kettő váltószög. Így $R$ rajta van a háromszög $B$-ből induló szögfelezőjén is, tehát valóban a beírt kör középpontja.