Feladat: 1973. évi Nemzetközi Matematika Diákolimpia 21. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1975/április, 163 - 164. oldal  PDF  |  MathML 
Témakör(ök): Síkbeli ponthalmazok távolsága, Magasságvonal, Thalesz-kör, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1973/szeptember: 1973. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldást két lépésben végezzük el. Először megmutatjuk, hogy van olyan legrövidebb út, amelyen a háromszög A csúcsából kiindulva a B és C csúcspont ellenőrizhető. Ezután azt látjuk be, hogy ezen az úton haladva a háromszög minden pontja beleesik a műszer hatósugarába.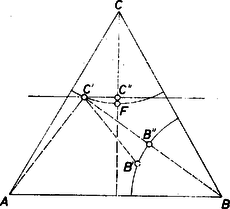
A magasság felét válasszuk egységnek (ekkor a háromszög oldala  43). Ahhoz, hogy a B és C pontot ellenőrizzük, el kell jutnunk a B és C körüli, 1 sugarú körvonal valamely B', ill. C' pontjába. Feltehető, hogy a katona a C' pontot érinti előbb, és így azt kell vizsgálnunk, hogy AC'¯+C'B'¯ miko minimális.

 

 

1. ábra
 

Rögzített C' esetén C'B'¯ akkor legkisebb, ha B' a C'B szakasz és a B körüli körvonal B'' metszéspontjába esik, hiszen egyébként C'B'¯+B'B¯>C'B¯=C'B''¯+B''B¯ és B'B¯=1=B''B¯. Feltehetjük tehát, hogy C'-től a katona a C'B szakaszon halad tovább. Ha útját a B pontig folytatná, akkor C' helyétől függetlenül mindig egységnyivel több utat tenne meg, azaz felhasználva, hogy AC'¯+C'B''¯ ugyanakkor minimális, mint AC'¯+(C'B''¯+1)=AC'¯+C'B'¯, azt kell eldöntenünk, hagy az A-ból B-be vezető és a C körüli kör egy pontját tartalmazó utak közül melyik a legrövidebb. Ehhez jegyezzük meg, hogy ha A-ból B-be úgy akarunk a legrövidebb úton menni, hogy közben egy AB¯-vel párhuzamos e egyenes valamely P pontját is érintjük, akkor P-nek az e egyenes és AB¯ felező merőlegesének Q metszéspontját kell választani (közismert megoldás: B-t e-re tükrözzük és A-t e tükörponttal összekötjük).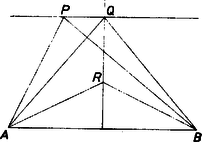
 

 

1. ábra
 

Másrészt, a felezőmerőlegesen mozgó R pontok esetén AR¯+RB¯ annál kisebb, minél közelebb van R az AB szakaszhoz. Ezek után a C', C'', F pontok helyzetét figyelve világos, hogy minimális hosszúságú utat akkor kapunk, ha a katona A-tól az F felezőpontba megy, majd onnan útját FB¯ mentén folytatja (2. ábra).
Ezután belátjuk, hagy ha most az AFB' út minden pontja köré egységnyi sugárral kört írunk, akkor ezek a körök az egész ABC háromszöglapot befedik.
 

 

3. ábra
 

Az AB szakasz T felezőpontját vetítsük merőlegesen BC-re és CA-ra, így kapjuk a Q és P pontot. Az F körüli egységnyi sugarú kör Q-n és P-n megy át (Thalész-tétel), így lefedi a TQCP négyszöget. Mivel FB'¯=FB¯-1=73-1<1, B' a QFT 60∘-os körcikk belsejében van (TQF szabályos háromszög, hiszen CTQ∢=60∘). Emiatt B'T¯<1 és BQ¯<1, és mivel B'B=1, a B' körüli kör lefedi a TBQ háromszöget. Hasonlóan, B' tükörképe A' körül egységnyi sugarú kört húzva ez a kör lefedi az ATP háromszöget. Tehát már az A', F, B' pontok körüli körök lefedik a háromszöget, és ezzel az állítást bebizonyítottuk.