Feladat:	1973. évi Nemzetközi Matematika Diákolimpia 13. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kiss Emil
Füzet:	1974/december, 205 - 206. oldal		PDF  |  MathML
Témakör(ök):	Szimmetrikus egyenletek, Negyedfokú (és arra visszavezethető) egyenletek, Szélsőérték-feladatok differenciálszámítás nélkül, Szélsőérték differenciálszámítással, ( x + 1/x ) > = 2 ( x > 0 ), Irracionális egyenlőtlenségek, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1973/szeptember: 1973. évi Nemzetközi Matematika Diákolimpia 13. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. $\begin{array}{c}{\displaystyle x^4+a{x}^3+b{x}^2+ax+1=0.}\end{array}$ (1) I. megoldás. Ha $a=a_0$ és $b=b_0$ olyan valós számok, amelyekre (1)-nek van egy $x_0$ valós gyöke, akkor $a=-a_0$, $b=b_0$ számok is olyanok, hiszen ekkor (1)-nek $-x_0$ is gyöke lesz. Mivel a vizsgálandó $a^2+b^2$ kifejezés értéke e két számpárra ugyanaz, feltehetjük, hogy $\begin{array}{c}{\displaystyle a\geqq 0.}\end{array}$ (2) (1) bal oldalának értéke $x=0$ mellett nem $0$, tehát (1) gyökei $0$-tól különbözőek, és gyökei az (1)-gyel ekvivalens $\begin{array}{c}{\displaystyle {\left(x+\frac{1}{x}\right)}^2+a\left(x+\frac{1}{x}\right)+b-2=0}\end{array}$ (3) egyenletnek is. Ennek viszont akkor és csakis akkor van valós gyöke, ha az ${\displaystyle \begin{array}{cc}\hfill {\displaystyle y^2+ay+b-2=0}\hfill & \text{(<mn>4</mn>)}\\ \hfill {\displaystyle x+\frac{1}{x}=y}\hfill & \text{(<mn>5</mn>)}\end{array}}$ egyenletekből álló rendszernek van valós gyöke. Rögzített $y$ mellett (5) $x$-re másodfokú egyenlet, amelynek akkor és csakis akkor van valós gyöke, ha $|y|\geqq 2$. Emiatt (3)-nak akkor és csakis akkor van valós gyöke, ha (4)-nek van $2$-nél nem kisebb abszolút értékű valós gyöke. 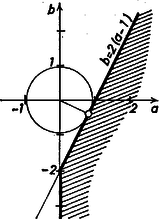(4) gyökeinek számtani közepe $-\frac{a}{2}<0$, tehát közülük a nagyobb abszolút értékű a kisebbik. Eszerint a keresett feltétel $\begin{array}{c}{\displaystyle \frac{-a-\sqrt[]{a^2-4b+8}}{2}\leqq -\mathrm{2,}}\end{array}$ ami ekvivalens a $\begin{array}{c}{\displaystyle 4-a\leqq \sqrt[]{a^2-4b+8}}\end{array}$ feltétellel. Ha $a\geqq 4$, akkor ez nyilván teljesül (feltéve, hogy a jobb oldali gyöknek van értelme), mert a bal oldalon nem pozitív, a jobb oldalon nem negatív szám áll. Az $a\geqq 4$ eset azonban a minimumhely keresése szempontjából kizárható, mert ekkor $a^2+b^2\geqq a^2\geqq 16$, és például $a=2$, $b=2$ esetén $x=-1$ megoldása (1)-nek, és ekkor $a^2+b^2=4+4=8<16$. Feltehetjük tehát, hogy $a<4$, ekkor $4-a>0$, és így most feltételünk ekvivalens a $\begin{array}{c}{\displaystyle {\left(4-a\right)}^2\leqq a^2-4b+8}\end{array}$ (6) feltétellel. (Ebből az alakból látható, hogy feltételünk azt is biztosítja, hogy (3)-nak legyen valós gyöke.) (6)-ból a $\begin{array}{c}{\displaystyle b\leqq 2\left(a-1\right)}\end{array}$ (7) feltételt kapjuk. Azt kell tehát meghatároznunk, hogy a (2) és (7) egyenlőtlenségeknek eleget tevő $\left(a\mathrm{,}b\right)$ számpárok közül $a^2+b^2$ értéke melyikre minimális. Egyenlőtlenségeink az $\left(a\mathrm{,}b\right)$ koordináta-rendszerben egy-egy félsíkot határoznak meg, $\left(a^2+b^2\right)$ pedig az $\left(a\mathrm{,}b\right)$ pontra nézve az origótól mért távolságnak a négyzete. Tehát a (2)‐(7) tartománynak az origóhoz legközelebbi pontját keressük: ez az origónak a $\begin{array}{c}{\displaystyle b=2\left(a-1\right)}\end{array}$ egyenesen levő vetülete. A vetület koordinátái $a=\frac{4}{5}$, $b=-\frac{2}{5}$, tehát $a^2+b^2$ minimuma $\frac{4}{5}$.     Kiss Emil (Budapest, Fazekas M. Gyak. Gimn., IV. o. t.)   II. megoldás. Az I. megoldásban láttuk, hogy azokat az $\left(a\mathrm{,}b\right)$ számpárokat kell vizsgálnunk, amelyekre (4)-nek van $2$-nél nem kisebb abszolút értékű valós gyöke. Jelöljük ezt a gyököt $u$-val: $|u|\geqq 2$, és jelöljük (4) másik valós gyökét $v$-vel. A gyökök és együtthatók összefüggése szerint $\begin{array}{c}{\displaystyle a=-u-v\mathrm{,}b-2=uv\mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle a^2+b^2={\left(u+v\right)}^2+{\left(uv+2\right)}^2=\left(u^2+1\right){\left(v+\frac{3u}{u^2+1}\right)}^2+u^2+4-\frac{9u^2}{\left(u^2+1\right)}\mathrm{.}}\end{array}$ Rögzített $u$ mellett ez akkor minimális, ha az első tag $0$, ekkor $\begin{array}{c}{\displaystyle a^2+b^2=\left(u^2+1\right)+\frac{9}{u^2+1}-6.}\end{array}$ Ennek keressük a minimumát az $u^2\geqq 4$ feltétel mellett. Megmutatjuk, hogy az $\begin{array}{c}{\displaystyle f\left(t\right)=t+\frac{9}{t}-6}\end{array}$ függvény monoton nő a $t\geqq 5$ szakaszon. Emiatt $f\left(t\right)$ a minimumát $t=5$ mellett veszi fel, és az  $f\left(5\right)=\frac{4}{5}$ érték egyben $a^2+b^2$ minimuma is a vizsgált feltétel mellett. Az $f\left(t\right)$ függvény deriváltja $\begin{array}{c}{\displaystyle f\text{'}\left(t\right)=1-\frac{9}{t^2}}\end{array}$ valóban pozitív $t\geqq 5$ mellett. Feladatunk megoldását ezzel befejeztük.