Feladat: 1972. évi Nemzetközi Matematika Diákolimpia 12. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1974/február, 58 - 60. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Téglalapok, Trapézok, Egyéb sokszögek hasonlósága, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1972/szeptember: 1972. évi Nemzetközi Matematika Diákolimpia 12. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Egy konvex négyszög akkor és csak akkor húrnégyszög, ha két szembenfekvő szögének összege 180∘. Legegyszerűbbnek tekinthetjük a négy derékszöggel bíró téglalap esetét, erre ugyanis már n=2 mellett helyes az állítás, mert bármelyik szemben levő oldalpárjával párhuzamos vágással két téglalapra vágható, és a kettévágás akárhányszor, bármelyik résztéglalapon megismételhető. ‐ Erre tekintettel elég bizonyítanunk a következő állítást: minden konvex négyszög szétvágható 4 darab húrnégyszögre úgy, hogy a részek közül legalább az egyik téglalap.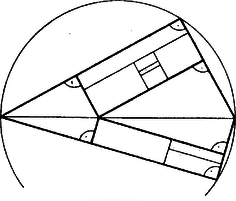
Ha a négyszögnek van derékszöge, de nem mindegyik szöge derékszög, akkor természetesen két szemben levő csúcsánál vannak a derékszögek, és a további két szög csúcsát összekötő átló Thalész tétele alapján a körülírt körnek átmérője és a négyszög belsejében halad (1. ábra).

 

 

1. ábra
 

Véve ennek bármely belső pontját, és merőleges szakaszt bocsátva belőle mind a négy oldalra, az adódó talppont mind a négy esetben belső pontja az illető oldalszakasznak. E szakaszok mentén szétvágva a négyszöget, tüstént látjuk, hogy két téglalap és két, a kiindulásihoz hasonló négyszög keletkezett, az állítás tehát helyes.
Ha pedig a négyszögnek egyik szöge sem derékszög, akkor van tompaszöge, és az ezzel szomszédos szögek egyike szintén tompaszög. Válasszuk úgy a betűzést, hogy a hegyesszögek csúcsai A és B, a tompaszögek csúcsai C és D. Állítsunk merőleges félegyenest C-ben a CB, és D-ben a DA oldalra, a négyszöget tartalmazó partjukon. Ezek a félegyenesek a CD szakasszal hegyesszöget zárnak be: γ-90∘-ot, illetve δ-90∘-ot, ezért metszik egymást egy M pontban. Vegyünk továbbá AB-vel párhuzamosan egy olyan egyenest, amely elválasztja a C, D pontpárt az A, B, M ponthármastól (2. ábra), és jelöljük az MC, MD szakaszon levő pontját E-vel, F-fel, továbbá ezek vetületét az AB egyenesen rendre E'-vel, F'-v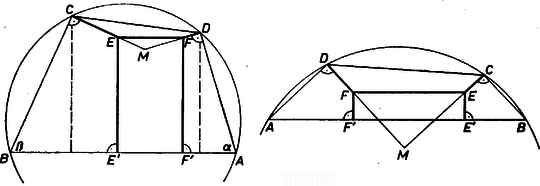el.
 

 

2. ábra
 

Megmutatjuk, hogy a CE, EF, FD, EE' és FF' szakaszok menti szétvágás megfelel célunknak.
Ugyanis β<90∘ miatt a CM félegyenes metszi a BA félegyenest, ezért M a C-ből AB-re bocsátott merőlegesnek, C "magasságvonalának'' B-t nem tartalmazó, az AD-t tartalmazó partján van; hasonlóan α<90∘ miatt M a D magasságvonalának az A-t nem tartalmazó, B-t és C-t tartalmazó partján van. Ezek szerint M e két magasságvonal közti sávban van, és itt van E, F is mint az MC, illetve MD szakasz pontja, továbbá E', F' is. Másrészt E, F az eredeti négyszögben is benne vannak, AB-nek a C-t és D-t tartalmazó partján.
A szétdarabolás részei húrnégyszögek: EFF'E' téglalap, AF'FD-ben és BE'EC-ben két‐két szemben levő csúcsnál derékszög van, végül a CEFD négyszögben
DCE∢+EFD∢=(γ-90∘)+{360∘-90∘-(180∘-α)}=γ+α=180∘.

Ezzel állításunkat bebizonyítottuk.
 

II. megoldás. A feladat állítása ugyancsak már n≧2 mellett érvényes akkor is, ha a kiindulási húrnégyszög szimmetrikus trapéz, mert ezt bármely az alapjaival párhuzamos szelője két szimmetrikus trapézra osztja. (Tulajdonképpen a szimmetrikus trapéznak speciális esete az I. megoldásban lényeges szerepet játszott téglalap.) Ennek alapján elég azt bizonyítanunk, hogy minden olyan ABCD konvex négyszög, melynek egymás utáni szögei α, β, γ és δ, és ezekre α+γ=180∘ (tehát egyszersmind β+δ=180∘ is), szétvágható két szimmetrikus trapézra és két olyan négyszögre, melyeknek egymás utáni szögei α, β, γ, δ. Egyszerűség kedvéért és az I. megoldásra is tekintettel kizárjuk a következő eseteket: α, β, γ, δ közt van derékszög, továbbá α=β és α=δ; így föltehetjük, hogy
α<β<90∘<δ<γ.(1)
Olyan pontot keresünk, ahonnan a keresett 4 vágás kiindulhat. Az egyik szimmetrikus trapéz egyik hegyesszögét B-ben kívánjuk úgy, hogy hosszabb alapja a BA oldal része legyen, szára a BC-nek része; a másik trapéz rövid alapja pedig a DA-nak, egyik szára a DC-nek legyen része. Mivel (1) szerint γ+β>180∘ és γ+δ>180∘, azért van az AD szakaszon olyan C1 pont és az AB szakaszon olyan C2, hogy CC1AC2 paralelogramma (3. ábra).
 

 

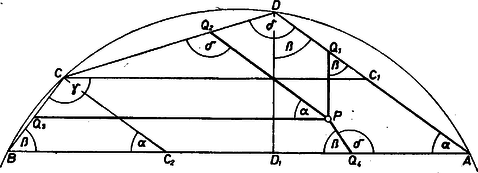3. ábra
 

Ennek minden belső pontján át húzható olyan párhuzamos AB-vel és AD-vel a két trapéz másik alapja céljára, amely B és C, illetve D és C között halad el, továbbá β>α alapján a B csúcsú trapéz másik szára is benne lesz a négyszögben. Avégett pedig, hogy a D csúcsú trapéznak a DA-n levő csúcsában is δ nagyságú szöge lehessen, a keresett pontnak abban DAD1 háromszögben is benne kell lennie, amelyre D1DA∢=β és D1 az AB oldal belső pontja. Ilyen D1 van, mert β<δ.
A paralelogrammának és a DAD1 háromszögnek van közös belső pontja, legyen egy ilyen P. Innen párhuzamost húzva D1D-vel, AD-vel, AB-vel, rendre az AD, DC, CB oldal egy‐egy belső pontjában érjük el a négyszög kerületét ‐ az ábrán rendre Q1, Q2, Q3 ‐, végül az AB oldal belsejében olyan Q4 is van, amelyre PQ4B∢=Q3BQ4∢=β. Így az AQ1PQ4 konvex négyszögben Q4-nél δ, Q1-nél β szög van, tehát P-nél γ, és a PQ3CQ2 négyszög szögei is rendre α, β, γ, δ.
Ezzel a bizonyítást befejeztük.
 

Megjegyzések. 1. Tulajdonképpen elég lett volna egy szimmetrikus trapézt biztosítani a 4 rész közt, amint ezt az I. megoldás végén a téglalappal tettük. Így viszont áttekinthetőbben biztosítottuk, hogy Q3PQ2∢=BAD∢ legyen.
2. Rámutatunk egy kifejezésre, ami első pillanatra csupán nyelvi kérdésnek látszik. Mindkét megoldásban ezzel vezettük be, hogy mit akarunk tenni: "elég bizonyítanunk, hogy ...'' . Sokszor halljuk, olvassuk efféle helyzetekben: "azt kell bizonyítanunk, hogy ...'' .
Ha ez a "kell'' itt helyes volna, akkor az I. megoldás célkitűzése ütné a II. megoldást, hiszen az utóbbi nem biztosítja az első szerint ‐ más szavakkal ‐ szükséges, nélkülözhetetlen téglalapot. (Fordítva viszont a szimmetrikus trapéz speciálisan lehet téglalap.)
Az "elég'' azt jelenti: így ‐ lehet, a "kell'' pedig valami ilyet: csak így lehet. A "kell''-et mondót valószínűleg semmi külső körülmény nem kényszeríti a tervezett eljárásra, legföljebb az a belső körülmény, hogy ő máshogy nem tudja. Aki pedig megelégszik az "elég''-gel, az ‐ esetleg ‐ látja, hogy máshogyan is lehetne. Oda jutottunk tehát, hogy ennek a különbségnek a tisztán látása igen is lényeges matematikai kérdés, jobb áttekintést mutat a kérdésben.
3. Kézenfekvő abból kiindulni, hogy a húrnégyszöget a köréje írt kör O középpontjából az oldalakra bocsátott merőlegesekkel vágjuk 4 részre. Ez azonban hármas esetszétválasztásra vezet aszerint, hogy O belső vagy kerületi pontja-e a négyszögnek, illetve ha O kívül van; így a bizonyítás a fentieknél valamivel hosszabb.