Kezdőlap


Feladat:	1968. évi Nemzetközi Matematika Diákolimpia 11. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1969/március, 99 - 100. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Szinusztétel alkalmazása, Koszinusztétel alkalmazása, Trigonometriai azonosságok, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1968/szeptember: 1968. évi Nemzetközi Matematika Diákolimpia 11. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy ha egy háromszög egyik szöge kétszer akkora, mint egy másik szöge, akkor a kétszer akkora szöggel szemben fekvő oldal mértani középarányos a másik említett szöggel szemben fekvő oldal és a további két oldal összege között. A szokásos jelölésekkel: ha $γ = 2 α$ , akkor

\begin{matrix} c^{2} = a (a + b) . \end{matrix}

(1)

Legyen az

A B C

háromszög

C

-ből induló szögfelezője

C D

, ekkor az

A C D

háromszög egyenlő szárú, és

D

-nél levő külső szöge

C D B ∢ = 2 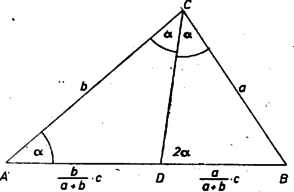α = A C B ∢

(

1

. ábra).

1. ábra

Így két-két szögük megegyezése alapján

A C B

és

C D B

hasonló háromszögek:

\begin{matrix} C B : A B = D B : C B . \end{matrix}

Itt a szögfelező osztásaránya alapján

\begin{matrix} D B & = \frac{a}{a + b} \cdot c, így \\ a : c & = \frac{a}{a + b} \cdot c : a, \end{matrix}

amiből állításunk következik.
Esetünkben

c > a

miatt csak

c = a + 1

vagy

c = a + 2

lehet. Az első esetben (1) alapján

\begin{matrix} b = \frac{c^{2} - a^{2}}{a} = \frac{2 a + 1}{a} = 2 + \frac{1}{a}, \end{matrix}

és ez csak

a = 1

esetén egész. Ekkor azonban

c = 2

és

b = 3

, e három szám nem teljesíti a háromszög egyenlőtlenséget.

c = a + 2

esetén

b

a nagyságra nézve középső oldal,

b = a + 1

, és így (1)-ből

\begin{matrix} {(a + 2)}^{2} = a (2 a + 1), a^{2} - 3 a - 4 = (a + 1) (a - 4) = 0. \end{matrix}

Ennek pozitív gyöke

a = 4

, és a feladat egyetlen megoldása:

a = 4

b = 5

c = 6

.
Ezzel az állítást bebizonyítottuk.

II. megoldás. Legyen továbbra is

γ = 2 α

. A

c

a

oldalpárra a sinustételt, majd az

a

oldalra a cosinustételt alkalmazva

\begin{matrix} \frac{c}{a} = \frac{sin γ}{sin α} = \frac{sin 2 α}{sin α} = 2 cos α = \frac{b^{2} + c^{2} - a^{2}}{b c}, \end{matrix}

alkalmas rendezéssel

\begin{matrix} (b - a) c^{2} = a (b^{2} - a^{2}) = a (b - a) (b + a), \end{matrix}

amiből ismét (1)-re jutunk, hiszen a vizsgálandó háromszögek nem egyenlő szárúak, egyszerűsíthetünk

b - a

-val. Tovább pedig az I. megoldás szerint haladhatunk.

Megjegyzések. 1. Látható, hogy az I. megoldás elemi meggondolásával egyszerűbben kaptuk (1)-et, mint a trigonometriai tételek alkalmazásával.
2. Könnyű belátni, hogy (1) megfordítása is helyes: ha (1) fennáll, akkor fennáll

γ = 2 α

is; más szóval a háromszögben a

c^{2} = a (a + b)

és a

γ = 2 α

összefüggés fennállása egymással ekvivalens állítások.
Mérjük rá

B C

-nek

C

-n túli meghosszabbítására a

C D = C A

szakaszt, ekkor (1) miatt az

A C D

egyenlő szárú háromszög köré írt kör érinti az

A B

egyenest

A

-ban (2. ábr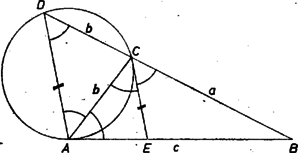a).

2. ábra

Ezért

C A B ∢ = C D A ∢

, mint a rövidebb

A C

íven nyugvó kerületi szögek. Párhuzamost húzva

C

-n át

D A

-val az

A B

-vel való

E

metszéspontig,

\begin{matrix} B C E ∢ = B D A ∢ = C A D ∢ = A C E ∢, \end{matrix}

tehát

B C A ∢ = 2 \cdot C D A ∢ = 2 \cdot C A B ∢

, amint állítottuk.
Hasonlóan trigonometriai számítással is könnyen bizonyítható az állítás megfordítása.