Kezdőlap


Feladat:	1966. évi Nemzetközi Matematika Diákolimpia 23. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bodor István
Füzet:	1968/április, 145 - 146. oldal		PDF \| MathML
Témakör(ök):	Középvonal, Számtani-mértani egyenlőtlenségek, Terület, felszín, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1966/szeptember: 1966. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelöljük a $B C$ , $C A$ , $A B$ oldal felezőpontját $A_{1}$ , $B_{1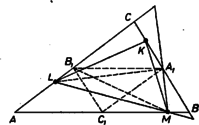}$ , $C_{1}$ -gyel.

Ha a kiszemelt csúcsok közül kettő az eredeti háromszög oldalainak közös csúcsú felén van, pl.

K

és

L

C A_{1}

-en, ill.

C B_{1}

-en, akkor

\begin{matrix} t_{C K L} \leq t_{C A_{1} B_{1}} = \frac{1}{4} t_{A B C} . \end{matrix}

Ha viszont

K

L

M

pl. rendre a

C A_{1}

A B_{1}

B C_{1}

szakasz belsejében van, akkor belátjuk, hogy

\begin{matrix} t_{K L M} > \frac{1}{4} t_{A B C} . \end{matrix}

Ebből már következik, hogy a másik három részháromszög valamelyikének területe kisebb az egész terület negyedénél, és ezt kell belátni.
Az

L M

egyenes a

B C

oldal

B

-n túli meghosszabbítását metszi, így a

t_{K L M}

csökken, ha

K

-t

A_{1}

-be visszük át. Hasonlóan

M A_{1}

A C

oldal

C

-n túli meghosszabbítását metszi, így

L

-et

B_{1}

-be víve tovább csökken a középháromszög területe, a keletkező

A_{1} B_{1} M

háromszög területe viszont az

A_{1} B_{1} C_{1}

háromszögével egyenlő, ami az

A B C

háromszög negyedrésze. A

K L M

háromszög területe tehát ennél nagyobb, amint állítottuk.

II. megoldás. Legyen

A M : A B = μ

B K : B C = ϰ

C L : C A = λ

, továbbá az

A B C

M A L

K B M

L C K

háromszög területe rendre

t

t_{a}

t_{b}

t_{c}

. Így a feltevés szerint

μ

ϰ

λ

1

-nél kisebb pozitív számok, továbbá

B M : A B = 1 - μ

C K : B C = 1 - ϰ

A L : C A = 1 - λ

.
Az

A

-nál közös szöggel bíró

M A L

és

B A C

háromszögek területének aránya

\begin{matrix} \frac{t_{a}}{t} = \frac{A M \cdot A L}{A B \cdot A C} = μ (1 - λ), \end{matrix}

(1)

ugyanígy

\begin{matrix} \frac{t_{b}}{t} = ϰ (1 - μ), \frac{t_{c}}{t} = λ (1 - ϰ), \end{matrix}

(2)

és ezeket összeszorozva

\begin{matrix} \frac{t_{a} t_{b} t_{c}}{t^{3}} = ϰ (1 - ϰ) λ (1 - λ) μ (1 - μ) . \end{matrix}

(3)

Ámde

\begin{matrix} 0 < ϰ (1 - ϰ) = \frac{1}{4} - {(\frac{1}{2} - ϰ)}^{2} \leq \frac{1}{4}, \end{matrix}

és ugyanígy

\begin{matrix} 0 < λ (1 - λ) \leq \frac{1}{4}, 0 < μ (1 - μ) \leq \frac{1}{4}, \end{matrix}

és ezeket összeszorozva kapjuk, hogy (3) bal oldala nem nagyobb

{1 / 4}^{3}

-nél. Ezért az (1) és (2) hányadosok közül legalább az egyik nem nagyobb

1 / 4

-nél, tehát a feladat állítása helyes.

Bodor István (Veszprém, Lovassy L. Gimn.)

Megjegyzés. Ajánljuk az érdeklődőknek a II. megoldás egybevetését az 1961. évi Kürschák József matematikai tanulóverseny 3. feladatára lapunkban¹ megjelent megoldásokkal.

¹Hajós György: Az 1961. évi Kürschák József matematikai tanulóverseny feladatainak megoldása, K. M. L. 24 (1962) 98‐107. o., szorosabban 101‐104. o.