Kezdőlap


Feladat:	1962. évi Nemzetközi Matematika Diákolimpia 24. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Szidarovszky Ferenc
Füzet:	1963/november, 109 - 113. oldal		PDF \| MathML
Témakör(ök):	Szabályos tetraéder, Tetraéderek, Hozzáírt körök, Beírt kör, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1962. évi Nemzetközi Matematika Diákolimpia 24. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Azon, hogy egy $t$ egyenes és egy $G$ gömb érintik egymást a $T$ pontban, azt értjük, hogy $t$ -nek és $G$ -nek egyetlen közös pontja $T$ . Bármely a $t$ -n átmenő $S$ sík $G$ -ből egy $k$ kört metsz ki ‐ kivéve a $T$ -hez tartozó gömbsugárra merőleges síkot, $G$ -nek $T$ -beli érintősíkját, amelynek $G$ -vel egyetlen közös pontja $T$ . Minden ilyen $k$ kör és $t$ ugyancsak érintik egymást $T$ -ben. Valóban, $T$ közös pontja $t$ -nek és $k$ -nak, de több közös pontjuk nincs, mert ha volna, ez $t$ -nek és $G$ -nek is közös pontja volna.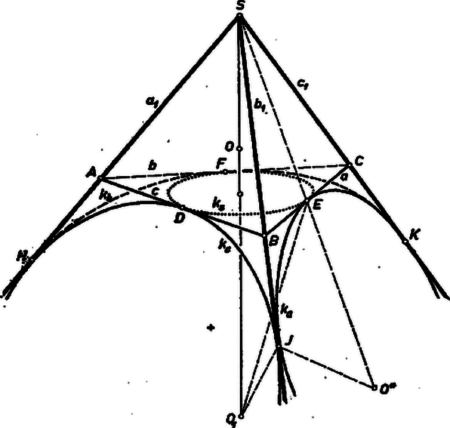
Legyen $G_{1}$ az $S A B C = N$ tetraéder valamennyi élét érintő öt gömb egyike, legyen az érintési pont az $A B$ , $B C$ , $C A$ , $S A$ , $S B$ , ill. $S C$ élen rendre $D$ , $E$ , $F$ , $H$ , $J$ , ill. $K$ , legyen továbbá $G_{1}$ -nek az $A B C$ , $S A B$ , $S B C$ , $S C A$ lappal való metszésvonala rendre a $k_{s}$ , $k_{c}$ , $k_{a}$ , ill. $k_{b}$ kör. Ezek valóban körök ‐ mert pl. $k_{s}$ átmegy a $D$ , $E$ , $F$ pontokon, ezek pedig nem eshetnek egybe, mert nincs az $A B$ , $B C$ , $C A$ egyeneseknek közös pontjuk. Így a $4$ kör rendre érinti az $A B C$ , az $S A B$ , az $S B C$ , ill. az $S C A$ háromszög oldalegyeneseit, és ezért rendre azonos a megfelelő háromszögbe beírt körrel, vagy valamelyik hozzáírt (külső érintő) körrel. Ismeretes, hogy a beírt kör mindegyik oldalegyenest az oldalszakaszon érinti (mind a három érintési pont belső), a 3 hozzáírt kör pedig az oldalegyenesek egyikét az oldalszakaszon érinti, a további kettőt pedig az előbbi szakasz végpontjain túli félegyenesükön (1 belső és 2 külső érintési pont).

1. ábra

Vegyük sorra a körök beírt, ill. hozzáírt voltára lehetséges kombinációkat. Tegyük fel, hogy

k_{s}

A B C

háromszögben beírt kör ‐ vagyis

D

E

F

a megfelelő oldalszakaszon van ‐, és legyen

H

S A

szakasz

A

-n túli meghosszabbításán (1. ábra). Így

k_{c}

S A B

háromszög

A B

oldalához,

k_{b}

pedig az

S A C

háromszög

A C

oldalához hozzáírt külső érintő kör, ezért

J

S B

él

B

-n túli,

K

pedig az

S C

-nek

C

-n túli meghosszabbításán van, tehát

k_{a}

ugyancsak hozzáírt kör, vagyis

G_{1}

N

lapjaiból 1 belső és 3 hozzáírt kört metsz ki. ‐ További 3 ilyen gömb (

G_{2}

G_{3}

G_{4}

) úgy adódik, ha rendre

k_{a}

-t,

k_{b}

-t,

k_{c}

-t vesszük beírt körnek, és egy további érintési pontot egy él meghosszabbításán választunk. ‐ Ha pedig

k_{s}

ismét beírt kör és

H

S A

szakasz pontja (2. ábra), akkor

k_{c}

és

k_{b}

is beírt kör, és így

k_{a}

is, ez a

G_{5}

gömb

N

minden lapjából beírt kört metsz ki. ‐ Nem lehet mind a négy kör hozzáírt kör, mert ha abból indulunk ki, hogy

k_{a}

S B C

háromszögnek pl. a

B C

oldalához hozzáírt köre (1. ábra), akkor

E

B C

szakaszon van,

J

és

K

pedig

B C

-nek

S

-sel ellentétes oldalán, ezért

k_{b}

már csak az

A C

oldalhoz,

k_{c}

pedig csak az

A B

-hez hozzáírt kör lehet, viszont

F

A C

D

A B

szakaszon van, ezért

k_{s}

beírt kör. Nincs tehát 5-nél több lehetőség az összes éleket ‐ vagy meghosszabbításukat ‐ érintő gömbre.
Megmutatjuk, hogy ha mind az

5

gömb létezik, akkor

N

összes élei egyenlők; így

N

lapjai szabályos háromszögek és

N

szabályos tetraéder. A körhöz külső pontból húzott érintőszakaszok egyenlősége alapján

N

egyes csúcsaiba befutó 3 élegyenesen az érintési szakaszokra fennáll:

\begin{matrix} S H = S J = S K, A D = A F = A H, & (1) \\ B D = B E = B J, C E = C F = C K . \end{matrix}

Ezek alapján bármelyik él hossza kifejezhető más három él hosszával, és a négy él között összefüggést kapunk.

G_{1}

-ből (1. ábra)

\begin{matrix} A B & = A D + D B = A F + J B = (A C - C F) + (S J - S B) = \\ = A C - S B + (S K - C K) = A C - S B + S C, \end{matrix}

tehát

\begin{matrix} A B - S C = A C - S B, \end{matrix}

(2a)

és hasonlóan (

A F

helyett

A H

-val,

J B

helyett

E B

-vel kezdve)

\begin{matrix} A B - S C = B C - S A . \end{matrix}

(2b)

A (2), (3) egyenlőség‐pár

G_{1}

létezésének szükséges feltétele. A beírt kört tartalmazó

A B C

lapot alaplapnak,

N

többi lapjait oldallapnak véve ezt kaptuk: külső élérintő gömb létezéséhez szükséges, hogy bármelyik oldalélt a szemben fekvő alapélből kivonva ugyanaz a különbség adódjék. Legyen röviden

B C = a

C A = b

A B = c

S A = a_{1}

S B = b_{1}

S C = c_{1}

, ekkor (2a) és (2b) így alakul:

\begin{matrix} a - a_{1} = b - b_{1} = c - c_{1} . \end{matrix}

(2)

2. ábra

S B C

lapból

k_{a}

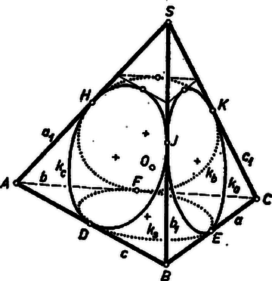beírt kört, a többiekből hozzáírt kört kimetsző

G_{2}

gömb esetében az alapélek

a

b_{1}

és

c_{1}

, ezért (2)-ből

\begin{matrix} a - a_{1} = b_{1} - b = c_{1} - c . \end{matrix}

(3)

Ezt (2)-vel egybevetve

G_{1}

és

G_{2}

egyidejű létezésének feltétele

b - b_{1} = 0

, vagyis

\begin{matrix} a = a_{1}, b = b_{1}, c = c_{1} . \end{matrix}

(4)

G_{3}

és

G_{4}

létezését (

G_{1}

és

G_{2}

mellett) feltételezve már nem kapunk újabb feltételeket.

G_{5}

létezéséből (2. ábra)

\begin{matrix} A B = A D + D B = A F + B J = A C - C F + S B - J S = \\ = A C + S B - (C K + K S) = A C + S B - S C, \end{matrix}

tehát

A B + S C = A C + S B

, és hasonlóan

A B + S C = B C + S A

, összefoglalva

\begin{matrix} a + a_{1} = b + b_{1} = c + c_{1} . \end{matrix}

(5)

(4) és (5) szerint már

G_{1}

G_{2}

és

G_{5}

létezéséből következik az összes élek egyenlősége, amit bizonyítani akartunk.

b) Legyen most

N

egy szabályos tetraéder. A közéje írt gömb

O

középpontja minden oldaléltől egyenlő távol van, mert az

S O

tengely körül

120^{\circ}

-kal elforgatva

N

önmagába megy át, és így

O

és az

S O

egyenes minden pontja egyenlő távol van az

a

b

c

élektől, másrészt az

a_{1}

b_{1}

c_{1}

élektől is. Mivel az

A O

tengely körüli

120^{\circ}

-os forgás is önmagába viszi át

N

-et, ezért

O

a

és

b_{1}

éltől is egyenlő távol van, tehát mind a 6 éltől, a fenti

G_{5}

létezik.
Ha találunk

S O

-n még egy pontot, amely

a

-tól és

b_{1}

-től egyenlő távol van, az is egy kívánt gömbnek (szükségképpen egy külső élérintő gömbnek) a középpontja. ‐ Az

S B C

háromszög

B C

oldalához hozzáírt

k_{a}

kör

B C

-t ennek

E

felezőpontjában érinti,

S B

-n levő érintési pontja legyen

J

, középpontja

O^{*}

O^{*}

S E

egyenesen van, mert

S B C

egyenlő oldalú háromszög.

S E

benne van

N

-nek

O S A

szimmetriasíkjában, amely merőleges az

S B C

lapra. Így az

O^{*}

-ban

S B C

-re állított merőleges is benne van az

O S A

síkban, tehát metszi az

S O

tengelyt egy

O_{1}

pontban. Erre nézve

O_{1} E

és

O_{1} J

egyenlők, mert átfogók az

O_{1} O^{*} E

és

O_{1} O^{*} J

derékszögű háromszögekben, amelyekben az

O_{1} O^{*}

befogó közös, és az

O^{*} E

O^{*} J

befogók egyenlők.

O_{1} E

adja

O_{1}

-nek

a

-tól való távolságát, mert

B C

merőleges az

O_{1}

-et tartalmazó

O S A

szimmetriasíkra;

O_{1} J

pedig

O_{1}

-nek

b_{1}

-től való távolságát, mert

S B

J

-ben érinti

k_{a}

-t, így az

O_{1}

körül

O_{1} J

sugárral írt

G_{1}

gömböt is, amely tartalmazza

k_{a}

-t.

O_{1}

-ből a szabályos tetraéder szimmetriáival az

A O

B O

C O

tengelyeken kapjuk a további

G_{2}

G_{3}

G_{4}

élérintő gömbök középpontját. Ezzel az állítást bebizonyítottuk.

Megjegyzések. 1. A b) részben

G_{5}

létezéséből

G_{1}

létezését így is beláthatjuk: Vegyük a

G_{5}

által az

S

-ben összefutó lapsíkokból kimetszett körökhöz az

A B

B C

C A

egyenessel párhuzamos érintőt (2. ábra). Ezek a szimmetria miatt az

S A

S B

S C

éleket páronként egybeeső pontokban metszik. Ezek és

S

egy szabályos tetraéder csúcsai, ennek élei érintik

G_{5}

-öt, éspedig 3 az élszakaszon, 3 a meghosszabbításon.

Szidarovszky Ferenc (Budapest, Fazekas M. gyak. g. IV. o. t.)

2. Láttuk, hogy

G_{1}

G_{2}

és

G_{5}

létezése ‐ vagyis két külső és egy belső élérintő gömb ‐ már biztosítja, hogy

N

csak szabályos lehet. Kérdezhetjük: elég-e három külső élérintő gömb létezése a szabályosság biztosításához, lehet-e szűkíteni a feltevést?
Könnyű belátni, hogy nem lehet.

k_{b}

-t beírt körnek, a többi hármat hozzáírt körnek véve (2)-ből a feltétel

a_{1} - a = b - b_{1} = c_{1} - c

és ez (4) miatt teljesül, ekkor létezik

G_{3}

is. (4) viszont akkor is teljesül, ha

a

b

c

egy nem szabályos háromszög oldalai, és a szemben fekvő oldalélek hossza rendre ugyancsak

a

b

c

. Ilyen tetraéderben létezik 4 külső élérintő gömb, ellenben nem létezik belső élérintő gömb, mert (5) nem teljesül. (A mondott tulajdonságú tetraéder létezik, ha

a

b

c

hegyesszögű háromszöget határoznak meg. Ezt a több érdekes tulajdonsággal bíró négylapot a kristálytanban szfenoidnak nevezik.)

3. Hasonlóan nyerjük (2) és (5) egybevetéséből, hogy egy belső és egy külső élérintő gömb létezése esetén a tetraéder szabályos háromoldalú gúla:

a = b = c

és

a_{1} = b_{1} = c_{1}