Kezdőlap


Feladat:	1962. évi Nemzetközi Matematika Diákolimpia 23. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1963/október, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Egyenlő szárú háromszögek geometriája, Körülírt kör középpontja, Beírt kör középpontja, Thalesz-kör, Síkgeometriai számítások trigonometria nélkül háromszögekben, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1962. évi Nemzetközi Matematika Diákolimpia 23. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha a háromszög egyenlő oldalú, akkor a két kör középpontja egybeesik és egyben a háromszög súlypontja is. Így $r = 2 ϱ$ , mert $r$ -et a súlyvonalnak a csúcs felé eső 2/3 része adja, $ϱ$ -t pedig a súlyvonalnak az oldal felé eső 1/3 része. A bizonyítandó egyenlőség fennáll, mert mindkét oldala 0.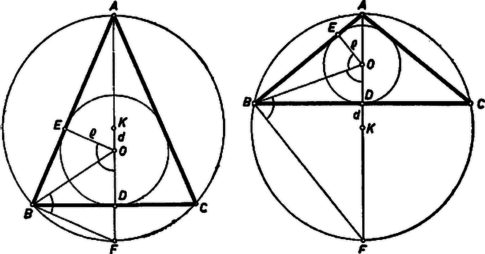

Legyen az

A B C

háromszögben

A B = A C

, a beírt kör középpontja

O

B C

-n és

A B

-n levő érintési pontja

D

, ill.

E

, a körülírt kör középpontja

K

, és

A

-val átellenes pontja

F

. A

B A C

szög

A O

felezője azonos az

A F

szimmetriatengellyel, így az

A E O

és

A B F

háromszögek hasonlók, mert

A

-nál levő szögük közös, másrészt az érintés, ill. Thalész tétele miatt

O E

is,

F B

is merőleges az

A B

szárra. Ezért

\begin{matrix} A O : A F = O E : F B . \end{matrix}

(2)

F B O

háromszög egyenlő szárú. Ugyanis

O E

és

F B

párhuzamosak, ezért

O B F

és

B O E

váltószögek, egyenlők, az utóbbi pedig egyenlő a

B O D = B O F

szöggel, mert

D

E

tükörképe a

B O

szögfelezőre. Így

F B = F O

, tehát (2)-ből

\begin{matrix} A O \cdot F B = A O \cdot F O = A F \cdot O E = 2 r ϱ . \end{matrix}

(3)

K

középpont a

2 r

hosszúságú

A F

szakasz középpontja, és

O

is ezen a szakaszon van, az egyik végponttól

r + d

, a másiktól

r - d

távolságra, tehát (3)-ból

\begin{matrix} r^{2} - d^{2} = 2 r ϱ . \end{matrix}

(4)

Az (1) állítás innen átalakítással adódik.

Szilágyi Tivadar (Budapest, II. Rákóczi F. g. III. o. t.)

Megjegyzések. 1. A megoldók nagy része a fentinél több számítással jutott eredményre. Egyenleteket írtak fel az

a

alap, a

b

szár, az

m

magasság, a

2 s

kerület és a

t

terület, valamint a két sugár között. Számos dolgozat nem vette azonban figyelembe

K

és

O

minden lehetséges elhelyezkedését.
2. Néhányan bebizonyították, hogy (1) minden háromszögre érvényes. ¹

¹V. ö. Kürschák‐Hajós‐Neukomm‐Surányi: Matematikai Versenytételek I. o. Középiskolai Szakköri Füzet (Tankönyvkiadó, Budapest 1955) 41. o.