Kezdőlap


Feladat:	1961. évi Nemzetközi Matematika Diákolimpia 22. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1962/szeptember, 20 - 22. oldal		PDF \| MathML
Témakör(ök):	Súlyvonal, Középvonal, Középponti és kerületi szögek, Középpontos tükrözés, Trigonometriai azonosságok, Apollóniusz-kör, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Nemzetközi Matematika Diákolimpia 22. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B$ szakasz középpontját $P$ -vel jelölve az $A B M$ háromszög $M P$ súlyvonala egyben az $A B C$ háromszögnek középvonala, s így $b / 2$ hosszúságú. Ennek alapján ez a háromszög megszerkeszthető: az $A B = c$ szakaszt felvéve $M$ számára egy mértani hely az $A B$ szakasz $ω$ nyílású $i$ látószögköríve, és egy másik a $P$ körül $b / 2$ sugárral írt $k$ kör. (Elég mindkettőt az $A B$ egyenes egyik partján megszerkeszteni, ti. amelyen $C$ -t kapni kívánjuk; így az $A B$ -re szimmetrikus megoldás felesleges előállítását elkerüljük.) Ezután $C$ -t mint $B$ tükörképét kapjuk az $M$ pontr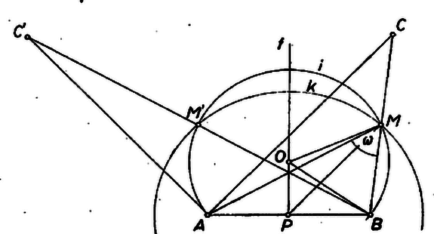a.

A szerkesztés helyessége nyilvánvaló. A megoldások száma 2, 1, vagy 0,

i

és

k

közös pontjainak száma szerint. 2 megoldás esetén az

A B M

és

B A M'

háromszögek az

A B

szakasz

f

felező merőlegesére tükrösek, és így egybevágók, az

A B C

és

A B C'

háromszögek azonban nem egybevágók.
Az

A M B

és

A M C

háromszögekben az

M A

oldal közös,

M B = M C

, a közbezárt szögek közül

A M B = ω

hegyesszög, ezért

A M C

szög tompaszög, így

A B < A C

, másképpen

\begin{matrix} c < b . \end{matrix}

(2)

Legyen az

i

körív középpontja O. Ha az

M

metszéspont létrejön, akkor

\begin{matrix} P O + O M \geq P M = \frac{b}{2} . \end{matrix}

(3)

Mivel

ω

hegyesszög, azért

O

A B

egyenesnek ugyanazon az oldalán van, mint

i

. Így a középponti és kerületi szögek közti összefüggés szerint

P O B ∢ = ω

, tehát

\begin{matrix} P O = P B ctg ω = \frac{c}{2} ctg ω, O M = O B = \frac{P B}{sin ω} = \frac{c}{2 sin ω} . \end{matrix}

Ezeket (3)-ba beírva (és a két oldalt felcserélve)

\begin{matrix} \frac{b}{2} \leq \frac{c}{2} (ctg ω + \frac{1}{sin ω}) = \frac{c}{2} \cdot \frac{1 + cos ω}{sin ω} = \frac{c}{2} \frac{2 cos^{2} \frac{ω}{2}}{2 sin \frac{ω}{2} cos \frac{ω}{2}} = \frac{c}{2 tg \frac{ω}{2}}, \end{matrix}

ugyanis

\begin{matrix} 1 + cos ω = sin^{2} \frac{ω}{2} + cos^{2} \frac{ω}{2} + cos^{2} \frac{ω}{2} - sin^{2} \frac{ω}{2} = 2 cos^{2} \frac{ω}{2} . \end{matrix}

A nyert egyenlőtlenség (1) bal oldalának átrendezett alakja. Ennek teljesülnie kell, ha a háromszög szerkeszthető. Fordítva, ha a nyert egyenlőtlenség teljesül, akkor (3) is, de akkor a

P

-ben

A P

-re emelt merőleges előbb metszi

i

-t, mint

k

-t, viszont (2) folytán

A

és

B

, az

i

körív végpontjai,

k

belsejében vannak, tehát

i

-nek és

k

-nak van közös pontja.

Udvardy Antal (Budapest, Táncsics M. g. III. o. t.)

Megjegyzés.

C

-t az

M

pont megszerkesztése nélkül is megkaphatjuk, ha ti. a

P B M

háromszögnek a B középpontból 2-szeresre nagyított képét szerkesztjük

Nárai György (Budapest, Bem J. g. III. o. t.)

II. megoldás. Húzzuk meg egy tetszés szerinti

B^{*} C^{*}

szakasz

M^{*}

felezőpontjából az

M^{*} B^{*}

-gal

ω

szöget bezáró félegyenest. Messe ezt a

B^{*}

és

C^{*}

alappontokhoz és a

c : b

aránymutatóhoz tartozó Apollóniosz kör

A^{*}

-ban. Ekkor

A^{*} B^{*} C^{*}

a keresetthez hasonló háromszög.

A^{*}

-tól

B^{*}

, ill.

C^{*}

felé felmérve az

A^{*} B = c

, ill.

A^{*} C = b

szakaszt, az

A^{*} B C

háromszög nyilvánvalóan megfelelő.
Megmutatható, de elég sok számítást igényel, hogy a félegyenes és a kör közös pontja létezésének feltétele éppen az állításbeli (1).

Bodoky Andrea (Budapest, Teleki Blanka lg. IV. o. t.)