Kezdőlap


Feladat:	1960. évi Nemzetközi Matematika Diákolimpia 13. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Kiss Ildikó , Kovács Imre , Molnár Emil , Sebestyén Mihály , Urbán László
Füzet:	1961/október, 53 - 56. oldal		PDF \| MathML
Témakör(ök):	Szögfüggvények, síkgeometriai számítások, Koszinusztétel alkalmazása, Egyenlő szárú háromszögek geometriája, Derékszögű háromszögek geometriája, Háromszögek egybevágósága, Trigonometriai azonosságok, Háromszögek hasonlósága, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):	Feladatok: 1960/október: 1960. évi Nemzetközi Matematika Diákolimpia 13. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A semmitmondó $n = 1$ esetet figyelmen kívül hagyjuk, mert ekkor $α = 90^{\circ}$ , és így sem $tg α$ , sem a jobb oldalon álló hányados nincs értelmezve. ‐ Legyen az átfogónak az $F$ felezőpontot tartalmazó szakasza $P Q$ úgy, hogy a pontok sorrendje az átfogón 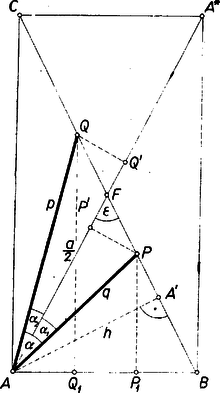$B$ , $P$ , $F$ , $Q$ , $C$ . Legyen $A P = q$ és $A Q = p$ .

Mivel

P Q = a / n

és az

A P Q

háromszögnek a

P Q

alaphoz tartozó magassága

h

, azért e háromszög területét kétféleképpen kifejezve

\begin{matrix} \frac{a}{n} \cdot \frac{h}{2} = \frac{p q}{2} sin α, és innen sin α = \frac{a h}{n p q} . \end{matrix}

Másrészt a koszinusz-tétellel

\begin{matrix} cos α = \frac{p^{2} + q^{2} - \frac{a^{2}}{n^{2}}}{2 p q}, és így tg α = \frac{2 a h}{n (p^{2} + q^{2} - \frac{a^{2}}{n^{2}})} . \end{matrix}

p^{2} + q^{2}

összeget kifejezhetjük az adatokkal abból, hogy

F

a részekre osztott

B C

átfogó középső

P Q

szakaszát is felezi, tehát

P F = F Q = a / 2 n

, másrészt, hogy

A F = a / 2

. Legyen

A F P ∢ = ε

, ekkor

A F Q ∢ = 180^{\circ} - ε

, ezért az

A Q F

és

A P F

háromszögekből a koszinusz-tétellel

\begin{matrix} p^{2} = {(\frac{a}{2})}^{2} + {(\frac{a}{2 n})}^{2} + 2 \cdot \frac{a}{2} \cdot \frac{a}{2 n} cos ε, \\ q^{2} = {(\frac{a}{2})}^{2} + {(\frac{a}{2 n})}^{2} - 2 \cdot \frac{a}{2} \cdot \frac{a}{2 n} cos ε, \end{matrix}

tehát

\begin{matrix} p^{2} + q^{2} = 2 [{(\frac{a}{2})}^{2} + {(\frac{a}{2 n})}^{2}] = \frac{a^{2}}{2} + \frac{a^{2}}{2 n^{2}} = \frac{(n^{2} + 1) a^{2}}{2 n^{2}} . \end{matrix}

(1)

Most már folytatólag

\begin{matrix} tg α = \frac{2 a h}{\frac{(n^{2} + 1) a^{2}}{2 n} - \frac{a^{2}}{n}} = \frac{4 n h}{(n^{2} - 1) a} . \end{matrix}

Urbán László (Székesfehérvár, József A. g. IV. o. t.)

Megjegyzés. (1)-et abból is megkaphatjuk, hogy véve

A

-nak

F

-re vonatkozó

A^{*}

tükörképét az

A P A^{*} Q

négyszög paralelogramma, melynek oldalai

p

és

q

, átlói

2 A F = a

és

P Q = a / n

, és így az 1006. feladat segédtétele szerint¹

\begin{matrix} a^{2} + \frac{a^{2}}{n^{2}} = 2 (p^{2} + q^{2}) . \end{matrix}

Molnár Emil (Győr, Révai M. g. IV. o. t.)

II. megoldás. Legyen

P A F ∢ = α_{1}

F A Q ∢ = α_{2}

P

Q

vetülete az

A F

egyenesen

P'

Q'

, végül

A

vetülete

B C

-n

A'

. Ha az

A B C

háromszög egyenlő szárú, akkor

A F ⊥ B C

h = a / 2

P'

és

Q'

F

-be esik,

α_{1} = α_{2} = α / 2

, és

tg α_{1} = tg α / 2 = 1 / n

, amiből

\begin{matrix} tg α = \frac{2 tg \frac{α}{2}}{1 - {tg}^{2} \frac{α}{2}} = \frac{\frac{2}{n}}{1 - \frac{1}{n^{2}}} = \frac{2 n}{n^{2} - 1}, \end{matrix}

ami az állításnak erre az esetre adódó egyszerűsödött alakja.
Ha

A B C

nem egyenlő szárú, akkor feltehetjük, hogy

A B < A C

. Így

B F A ∢ = 2 B C A ∢

hegyesszög, tehát

P'

A F

szakaszon,

Q'

pedig

F A^{*}

-on van. Nyilvánvaló, hogy az

F P P'

és

F Q Q'

derékszögű háromszögek egybevágók, és így

P P' = Q Q'

F P' = F Q'

, tehát a

P A P'

és

Q A Q'

derékszögű háromszögekből

\begin{matrix} tg α_{1} = \frac{P P'}{A P'} = \frac{P P'}{A F - F P'}, tg α_{2} = \frac{Q Q'}{A Q'} = \frac{P P'}{A F + F P'}, \end{matrix}

tehát

\begin{matrix} tg α = tg (α_{1} + α_{2}) = \frac{\frac{P P'}{A F - F P'} + \frac{P P'}{A F + F P'}}{1 - \frac{P P'^{2}}{A F^{2} - F P'^{2}}} = \frac{2 A F \cdot P P'}{A F^{2} - (F P'^{2} + P P'^{2})} = \\ = \frac{B C \cdot P P'}{A F^{2} - F P^{2}} = \frac{a P P'}{\frac{a^{2}}{4} - \frac{a^{2}}{4 n^{2}}} = \frac{4 n^{2} \cdot P P'}{(n^{2} - 1) a} . \end{matrix}

Másrészt az

F P P'

derékszögű háromszög hasonló

F A A'

-höz, mert

F

-nél levő szögük közös, ezért

\begin{matrix} \frac{P P'}{A A'} = \frac{F P}{F A} = \frac{a / 2 n}{a / 2} = \frac{1}{n}, tehát P P' = \frac{h}{n}, \end{matrix}

ezt

tg α

legutóbbi kifejezésébe helyettesítve az állítást kapjuk.

Kiss Ildikó (Budapest, Teleki Blanka lg. III. o. t.)

III. megoldás. Számíthatjuk

α

-t különbségként is, pl.

α = B A Q ∢ - B A P ∢

. Legyen

P

Q

vetülete

A B

-re

P_{1}

Q_{1}

; ekkor a

P_{1} B P

Q_{1} B Q

derékszögű háromszögek hasonlók

A B C

-höz, és átfogójuk a

B C

átfogó

n

-edrészének

(n - 1) / 2

-szöröse, ill.

1 + (n - 1) / 2 = (n + 1) / 2

-szöröse ‐ ugyanis a

B P

és

Q C

szakaszokba az

F

-et tartalmazó szakasz elvételével megmaradt

n - 1

számú szakasz fele-fele jut ‐, tehát 3

P_{1}

\frac{B P}{B C}

AC=

\frac{n - 1}{2 n}

AC,

Q_{1}

\frac{n + 1}{2 n}

AC,

P_{1}

B=A

Q_{1}

\frac{n - 1}{2 n}

AB,

Q_{1}

B=A

P_{1}

\frac{n + 1}{2 n}

AB, hiszen egyenlő és egyirányú szakaszoknak ugyanazon egyenesre való vetületei egyenlők. Ezekkel

\begin{matrix} tg B A Q ∢ = \frac{Q_{1} Q}{A Q_{1}} = \frac{n + 1}{n - 1} \cdot \frac{A C}{A B}, tg B A P ∢ = \frac{P_{1} P}{A P_{1}} = \frac{n - 1}{n + 1} \cdot \frac{A C}{A B}, \\ tg α = tg (B A Q ∢ - B A P ∢) = \frac{(\frac{n + 1}{n - 1} - \frac{n - 1}{n + 1}) \cdot \frac{A C}{A B}}{1 + \frac{A C^{2}}{A B^{2}}} = \frac{4 n A B \cdot A C}{(n^{2} - 1) B C^{2}} . \end{matrix}

Végül figyelembe véve, hogy az

A B \cdot A C

szorzat az

A B C

háromszög 2-szeres területét adja, ami az adatokkal kifejezve

a h

-val egyenlő, továbbá, hogy

B C = a

tg α

-nak az állításban szereplő kifejezésére jutunk.

Sebestyén Mihály (Szolnok, Verseghy F. g. III. o. t.)

Megjegyzések. 1. Számos dolgozat

α

-t az

A' A Q

és

A' A P

szögek különbségeként számította, sokan mások pedig a külső szög tétele alapján mint az

A P A'

és

A Q A'

szögek különbségét.
Ha az

A B

és

A C

befogók közt elég nagy a különbség, vagy ha

n

elég nagy szám, akkor

P

és

Q

valóban

A'

ugyanazon oldalára esnek, és

α

az előbb említett két szög különbsége. De

A'

szét is választhatja

P

-t és

Q

-t. Némelyek erre is kitértek,

A' P

-nek

A' Q

-hoz képest előjelet tulajdonítottak, hasonlóan az

A' A P

szöget forgásszögnek tekintették. Ezt a diszkussziót a III. megoldás elkerülte azzal, hogy a

P A Q

szögtartományon biztosan kívül eső

A B

irányt választotta alapiránynak. ‐ Az említett második számításmód mellett pedig gondolni kellett volna arra a lehetőségre is, ha

P

éppen

A'

-be esik, és így az

A' P A

(ill.

B P A

) szög derékszög, tangense nincs értelmezve.
2. Az átfogó osztás pontjai közül csak

P

és

Q

-t használtuk, és az

n

számot is csak annyiban, hogy

P Q : B C = 1 : n

. Ezért

n

nemcsak páratlan természetes szám lehet, hanem bármely 1-nél nagyobb pozitív szám. (

0 < n < 1

is lehet, vagyis

P Q > B C

. Szerk.) A kikötés csak az, hogy a

P Q

szakasz tükrös legyen

F

-re.

Kovács Imre (Békés, Szegedi Kis I. g. IV. o. t.)

¹Lásd K. M. L. 21 (1960) 20. o.