Feladat: 1959. évi Nemzetközi Matematika Diákolimpia 21. feladata Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Lakner József ,  Szekeres Veronika ,  Windisch Ferenc 
Füzet: 1960/május, 176 - 178. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek szerkesztése, Thalesz-kör, Súlyvonal, Középvonal, Derékszögű háromszögek geometriája, Pont körüli forgatás, Pont körre vonatkozó hatványa, Középponti és kerületi szögek, Háromszögek egybevágósága, Nemzetközi Matematikai Diákolimpia
Hivatkozás(ok):Feladatok: 1959/október: 1959. évi Nemzetközi Matematika Diákolimpia 21. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. A mértani középre vonatkozó adat kézenfekvővé teszi a szerkesztésnek számítással való előkészítését. Igyekszünk azonban geometriai meggondolások révén minél kevesebb számolással célhoz érni.

 

I. megoldás: Az AB=c átfogó ismeretében csak a derékszög C csúcsát kell megkapnunk. Erre egy mértani hely az AB átmérő fölötti Thalész-kör, a háromszög k körülírt köre. Az átfogó F felezőpontja egyben k középpontja, ezért a CF súlyvonal egyenlő k-nak r sugarával, az átfogó c/2 felével. Így a feltétel szerint
ab=(c/2)2=c2/4.
A bal oldal a háromszög kétszeres területét jelenti, az pedig másképpen cmc-vel egyenlő. Így cmc=c2/4-ből mc=c/4=r/2.
Ennek alapján a háromszöget a következőképpen szerkeszthetjük meg: az AB=2r átfogó felett megrajzoljuk a k Thalész-kört (elég az AB egyik oldalán levő felét, így megválasztva, hogy C-t melyik oldalon kívánjuk), ebből az AB-re merőleges FE sugárral kimetsszük az AB fölött r magasságban fekvő E pontot; végül FE-nek f felező merőlegesével k-ból kimetsszük C-t. A két metszéspont AB-nek FE=g felező merőlegesére tükrös, ezért az adódó két háromszög egybevágó.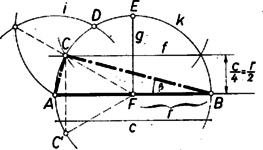
 
 
1. ábra
 

A nyert ABC háromszög megfelelő, mert derékszögű, továbbá c-re merőleges magassága r/2=c/4, így kétszeres területe c⋅c/4=c2/4, és ez egyenlő ab-vel. Innen a befogók mértani középarányosa: ab=c/2, és ezzel teljesül a követelmény, mert a kérdéses súlyvonal hossza ugyancsak c/2.
A C csúcsot mint k és f metszéspontját E birtokában f megrajzolása nélkül is megszerkeszthetjük. Mivel ugyanis k egy F körüli körív, így az E körül r sugárral rajzolt ív éppen C-t és g-re vonatkozó tükörképét metszi ki k-ból.
 

Szekeres Veronika (Makó, József A. Gimn. I. o. t.)

 

Megjegyzés. Tudva, hogy mc=c/4=r/2, meghatározhatjuk és megszerkeszthetjük a háromszög β szögét is. Jelöljük C tükörképét AB-re C'-vel. Ekkor a CFC' háromszög minden oldala r hosszúságú, tehát CFC'∢=60∘, így AFC∢=30∘ és a BCF egyenlő szárú háromszög alapon fekvő szögei, amelyek egyike β, 15∘-osak. ‐ Ennek alapján az AB=c szakasz F felezőpontja körül, és A végpontja körül r=c/2 sugárral k, ill. i kört rajzolunk; legyen ezek egyik metszéspontja D. A D körül r sugárral rajzolt körívnek i-vel való (F-től különböző) metszéspontját F-fel összekötő egyenes metszi ki k-ból a keresett C csúcsot.
 

II. megoldás: Forgassuk el a feltételnek megfelelő ABC háromszög BC befogóját az AB átmérő fölötti, C-t tartalmazó k félkörív E felezőpontja körül 90∘-kal (2. áb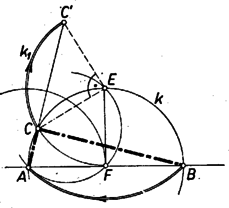ra).
 
 
2. ábra
 

Ekkor BC párhuzamos helyzetbe kerül AC-vel. B az elforgatáskor A-ba kerül, ezért C az AC egyenes egy C' pontjába kerül. Mivel a feladat feltétele szerint
AC⋅AC'=AC⋅BC=(c/2)2,
azért ‐ annak a tételnek az alapján, hogy a körhöz egy külső pontból húzott szelőn keletkezett szakaszok mértani közepe egyenlő a pontból a körhöz húzható érintővel ‐ az E pont körül C-n és C'-n át rajzolt k1 körhöz A-ból húzható érintők hossza c/2. Tehát az érintési pontokat az A körül c/2 sugárral rajzolt kör és az AE mint átmérő fölé rajzolt kör metszéspontjai adják. Ezek egyike az AB szakasz F felezőpontja, ezért k1 érinti F-ben AB-t, és így sugara EF=c/2. A C pontot tehát az E körül c/2 sugárral rajzolt kör metszi ki k-ból.
Az így szerkesztett C pont megfelel a feltételnek, mert a k1 kör AC-vel való másik metszéspontját C'-vel jelölve AC⋅AC'=(c/2)2. Másrészt AC' az E körüli 90∘-os elforgatással átvihető BC-be és így AC⋅BC=AC⋅AC'=(c/2)2.
 

Lakner József (Székesfehérvár, József A. g. II. o. t.)

 

III. megoldás: A szakaszok mértani közepére előbb idézett tétel szerint az AB-t F-ben érintő és C-n átmenő k2 kör BC-t (mint szelőt) másodszor abban a (B és C közti) G pontjában metszi, amelyre 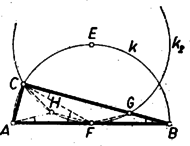BG=BF2/BC=c2/4a=b=AC (3. ábra).
 
 
3. ábra
 

A BFG szög k2-nek FG ívén fekszik, ezért egyenlő az FCB szöggel, és mivel a BFC háromszög egyenlő szárú (a BF és FC oldalak k sugarai), azért egyszersmind FBC∢=β-val, tehát BFG egyenlő szárú háromszög, GF=GB=b. Legyen az F-en át BC-vel húzott párhuzamosnak k2-vel való második metszéspontja H. Ez a párhuzamos felezi az AFC=2β szöget (középponti szög a k kör AC ívén), mert a HFA szög egyállású CBA∢=β-val, ennélfogva felezi k2-nek az AFC szög szárai közötti FC ívét is. Így a HF, HC húrok egyenlők, és mivel a GFHC idom húrtrapéz, azért HF=CH=FG=b. Ebből következik, hogy az AFH és FBG háromszögek egybevágók, mert két oldaluk és közbezárt szögük egyenlő, tehát AH=FG=b. Így pedig az ACH háromszög egyenlő oldalú, a HCA szög 60∘. Ebből HCG∢=FGC∢=AFC∢=30∘, eszerint k2 középpontjából az FC=r=c/2 húr 60∘-os szögben látszik, így k2 sugara egyenlő r-rel, tehát k2 azonos az előző megoldásbeli k1-gyel.
 

IV. megoldás: Kiszámíthatjuk a befogókat is. Feltehetjük, hogy a>b. Az ab=c2/4 egyenlőséget az ismeretlen a, b-re egyenletnek tekintve és az a2+b2=c2 püthagorászi egyenlőséggel összekapcsolva könnyen megoldható típusú egyenletrendszert kapunk. Az első egyenlet kétszeresét a másodikból kivonva, majd hozzáadva a-b-re, ill. a+b-re adódik egyenlet:
a2+b2-2ab=(a-b)2=c2-c2/2=c2/2,a2+b2+2ab=(a+b)2=c2+c2/2=3c2/2,
és innen, minthogy szakaszok pozitív különbségéről, ill. összegéről van szó:
a-b=c/2,a+b=c3/2,
amik egyszerűen megszerkeszthető hosszúságok. Innen megkaphatjuk a-t vagy b-t; de a-b-ből vagy a+b-ből, továbbá a c oldalból és a vele szemben fekvő γ=90∘ szögből a háromszög ismert módon közvetlenül is megszerkeszthető.
 

Windisch Ferenc (Budapest, József A. Gimn. II. o. t.)