Feladat: 1966. évi Matematika OKTV II. forduló 2. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1967/február, 49 - 54. oldal  PDF  |  MathML 
Témakör(ök): Húrnégyszögek, Tengelyes tükrözés, Középpontos tükrözés, Pont körre vonatkozó hatványa, Háromszögek hasonlósága, OKTV
Hivatkozás(ok):Feladatok: 1967/február: 1966. évi Matematika OKTV II. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az e egyenesnek a négyszög belsejébe eső szakasza PQ, és M felezze PQ-t. Ha e azonos a négyszög egyik átlójával, akkor a feladat állítása semmitmondó. Feltehetjük tehát, hogy e a két átló között halad, így a négyszöget szemközti oldalaiban metszi. Válasszuk úgy a betűzést, hogy P a négyszög BC, Q a DA oldalszakaszán legyen. Tükrözzük az A csúcsot a PQ szakasz t felező merőlegesére, kapjuk az A1 pontot. Megmutatjuk, hogy A1 rajta van az ABCD négyszög köré írt k 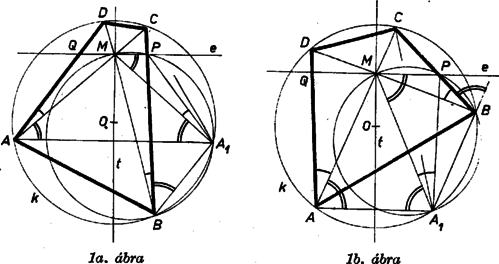körön.
AA1∥PQ, hiszen mindkettő merőleges t-re. PMA1∢=MA1A∢, mert váltószögek, MA1A∢=MAA1∢ a tükrözés miatt, és ez utóbbi azonos a CAA1 szöggel, tehát PMA1∢=CAA1∢. (Az 1.a-1.b ábrákon t szétválasztja A-t és B-t.) Az A1, B, P, M pontok egy körön vannak, hiszen

PBM∢=CBD∢=CAD∢=MAQ∢=MA1P∢,
egyrészt a kerületi szögek tétele, másrészt a tükrözés miatt, és mert az A1, B pontok az MP egyenesnek ugyanazon az oldalán vannak. Ha az A és B pontok az A1C egyenes azonos oldalán vannak, akkor a B és M pontok is ugyanazon az oldalán vannak az A1P egyenesnek, így az A1P szakasz a B és M pontokból egyenlő szögben látszik.
 
 

Mivel A1BP és A1BC szögek azonosak, a PMA1 és CAA1 szögek pedig egyenlőek, az A1C szakasz is ugyanakkora szögben látszik az A és B pontokból, A1 tehát valóban rajta van az A, B, C pontok által meghatározott k körön.
 

Ugyanezt kapjuk, ha az A1C egyenes elválasztja az A és B pontokat (1.b ábra). Ebben az esetben az A1P egyenes is elválasztja az M és B pontokat, az A1BP és PMA1 szögek tehát 180∘-ra egészítik ki egymást, így az A1BC és CAA1 szögek is 180∘-ra egészítik ki egymást, és A1 most emiatt lesz a k körön.
Hasonlóan adódik állításunk, ha A és B a t-nek ugyanazon oldalán van (2. ábra).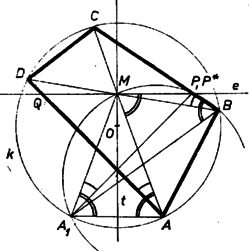
 
 
2. ábra
 

Mivel A1 a k körön van, az AA1 szakasz felezőmerőlegese, a t egyenes a k kör átmérője, így felezi a rá merőleges e egyenesre eső húrt, amint azt bizonyítanunk kellett.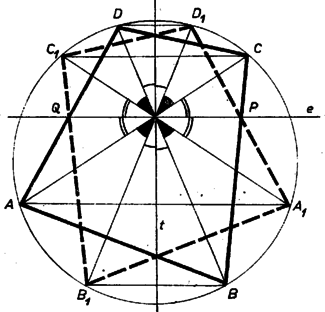
 
Megjegyzések. 1. Lényegében ugyanígy halad a megoldás, ha a t egyenest eleve az M-en átmenő átmérőnek vesszük fel (2. ábra). Ebben az esetben A1 nyilván a k körre kerül, ellenben bizonyítanunk kell, hogy PQ is merőleges t-re. Mivel ezt nehéz közvetlenül belátni, a versenyzők többsége a feladat állításának a fordítottját bizonyította, hogy ti. ha egy az M-en átmenő e egyenesnek M a körre eső húrját felezi, akkor felezi a négyszögbe eső szakaszát is. Ha M és k kör O középpontja azonos, akkor ‐ mint az könnyen látható ‐ minden egyenesnek megvan mindkét tulajdonsága. Ha M és O nem azonos, akkor M nyilván akkor felezi az e egyenesre eső húrt, ha e⊥OM. Ha tehát belátjuk egyrészt, hogy ebből következik, hogy M felezi az e egyenes négyszögbe eső szakaszát, másrészt, hogy olyan egyenes is csak egy van, amelyiknek a négyszögbe eső szakaszát M felezi, akkor e kettő együtt kiadja a feladat állításának a bizonyítását. Az első rész a fenti megoldáshoz hasonló módon bizonyítható: mivel PMA1∢=A1AC∢, az A1, B, P, M pontok egy körön vannak, tehát PA1M∢=PBM∢, viszont ez teljesül a Q pont tükrözéséből származó P* pontra is: P*A1M∢=PBM∢, P* tehát azonos P-vel. A második rész bizonyításával kapcsolatban a II. megoldás első mondataira utalunk.
 
 
3. ábra
 

2. Ha az egész négyszöget tükrözzük az OM egyenesre, akkor P és Q a megfelelő oldalak metszéspontja lesz, és azt kell megmutatnunk, hogy PQ⊥OM. Valóban, az M pontban keletkezett 12 szög közül a 3. ábrán azonosan jelzettekről könnyen kimutatható, hogy egyenlőek, amiből már következik az állításunk. Ebben az esetben azonban fel kell használnunk, hogy olyan egyenes, amelyen levő húrt M felezi, ill. olyan egyenes, amelynek a négyszögre eső szakaszát M felezi, csak egy van, mert csak ennek belátása után következik a feladatunk állítása abból, hogy az általunk adott konstrukció mellett a PQ egyenesnek mindkét tulajdonsága megvan.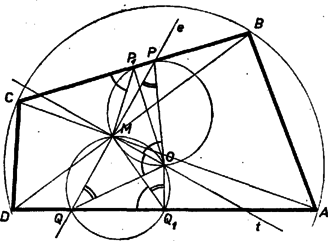
 
 
4. ábra
 

3. Azt viszont, hogy ha M felezi PQ-t, akkor a PQ szakasz t felező merőlegese átmegy a k kör középpontján, tükrözés nélkül is beláthatjuk (4. ábra). Legyen Q1 az AD, P1 a BC szakasz felezőpontja. Feltehetjük, hogy a Q1 pontból a DM szakasz látszik hegyesszög alatt, ekkor az AMD, BMC háromszögek hasonlósága miatt a P1 pontból ugyanakkora α szög alatt látszik a CM oldal. Attól függően, hogy a P, ill. a Q pont a P1C, ill. Q1D szakaszra esik-e vagy sem, az MP, ill. MQ szakasz vagy α, vagy 180∘-α szög alatt látszik a P1, ill. Q1 pontokból.
Keressük meg a t egyenesnek az e egyenes A és B csúcsokat tartalmazó oldalára eső félegyenesén azt az O pontot, ahonnan az MP és MQ szakaszok α szög alatt látszanak. Akkor az O, P, P1, M, ill. O, Q, Q1, M pontok egy‐egy körön lesznek, melyeknek OP és OQ átmérői, az OP1P, OQ1Q szögek tehát derékszögek, így O a k kör középpontjával azonos.
 

II. megoldás. Tükrözzük az ABCD négyszöget és a köré írható k kört a négyszög átlóinak M metszéspontjára. Ha M mindkét átlót felezi, a négyszög és a k kör önmagába megy át, ebben az esetben az M ponton átmenő egyeneseknek a négyszögbe és a körbe eső szakaszát is felezi M, állításunk tehát igaz. Ha M csak egy átlót felez, válasszuk úgy a betűzést, hogy ez az AC átló legyen, és teljesüljön, hogy BM<MD. Akkor a tükrözés során az A és C csúcsok helyet cserélnek, a B csúcs, és a belőle kiinduló AB, BC oldalak a négyszög belsejébe, a D csúcs és a belőle kiinduló CD, DA oldalak a négyszögön kívülre kerülnek, így csak az AC átlónak felezi M a négyszögbe eső darabját, AC viszont egyben a k-nak is húrja, állításunk tehát ismét nyilvánvaló.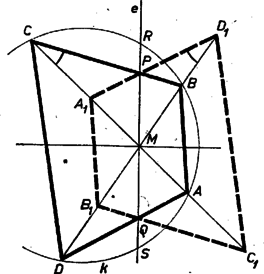
 
 
5. ábra
 

A továbbiakban feltehetjük tehát, hogy M egyik átlót sem felezi. Válasszuk úgy a betűzést, hogy az AC átlón A, a BD átlón B legyen az M-hez közelebbi csúcs (5. ábra). A tükrözés során kapott A1 és B1 csúcs az eredeti négyszög belsejében lesz, a C1, D1 csúcs pedig azon kívülre kerül, így csak a BC és A1D1, ill. DA és B1C1 szakaszok metszhetik egymást a tükrözött és az eredeti négyszög kerületén. Legyenek a metszéspontok P és Q, ekkor csak a PQ egyenesnek felezheti M a négyszögbe eső szakaszát. A kapott BD1P és A1CP háromszögek hasonlóak, hiszen P-nél levő szögük egyenlő és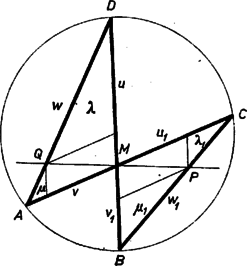
A1CP∢=ACB∢=ADB∢=A1D1B1∢=PD1B∢,
emiatt
A1PPC=BPPD1.
A tükrözés miatt viszont A1P=AQ és PD1=QD, tehát
AQ⋅QD=BP⋅PC,
azaz a P és Q pontoknak a k körre vonatkoztatott hatványuk egyenlő. (Ismeretes, hogy egy k körhöz adott P pontból húzott szelő darabjainak szorzata független a szelő választásától ‐ ezt a szorzatot nevezzük a P pont k körre vonatkozó hatványának.) Ebből már következik a bizonyítandó állítás, hiszen ha a PQ egyenes a k kört az R, S pontokban metszi, és PS>QS, akkor
RP⋅PS=RQ⋅QS,
és mindkét oldalból RP⋅QS-t levonva kapjuk, hogy
RP(PS-QS)=(RQ-RP)QS,
ahol PS-QS=PQ=RQ-RP, tehát valóban RP=QS, azaz RM=MS.
 
 
6. ábra
 

Megjegyzések. 1. Azt, hogy a P, Q pontok k-ra vonatkozó hatványa egyenlő, tükrözés nélkül is beláthatjuk.
Húzzunk P-n és Q-n át párhuzamosakat az AC, BD átlókkal (6. ábra), így az egymáshoz hasonló ADM, BCM háromszögek mindegyikét egy paralelogrammára és két háromszögre vágtuk fel. A keletkezett négy kis háromszög hasonló az eredeti háromszögekhez, a paralelogrammák is hasonlók, és mivel PM és MQ átlóik egyenlők, egybevágóak is. Legyenek az ADM és BCM háromszögek oldalai rendre u, v, w, ill. u1, v1, w1, és a DQ, QA, ill. CP, PB alapú kis háromszögek oldalai a megfelelő nagy háromszögek oldalainak rendre λ, μ, ill. λ1, μ1-szeresei. Az AC átlóval párhuzamos oldalt a DQ és PB alapú, a BD átlóval párhuzamos oldalt pedig a QA, PC alapú háromszögben felírva kapjuk, hogy
λv=μ1u1;μu=λ1v1,
ezeket összeszorozva
λμuv=λ1μ1u1v1.
Az ADM, BCM háromszögek hasonlósága miatt
u:w=u1:w1ésv:w=v1:w1,
ezt a két aránypárt összeszorozva kapjuk, hogy
uv:w2=u1v1:w12.
Ebből következik, hogy
λw⋅μw=λ1w1⋅μ1w1,
ami épp a bizonyítandó egyenlőség:
DQ⋅QA=CP⋅PB.

Beláthatjuk ezt a színusz‐tétel felhasználásával is (7. ábra):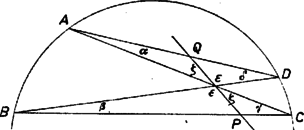
BPQD=BPMP:QDQM=sinεsinβ:sinεsinδ=sinζsinα:sinζsinγ=AQQM:PCMP=AQPC.
 
 
7. ábra
 

2. Ha felhasználjuk, hogy két egymást metsző körre azon pontok mértani helye, amelyeknek a két körre vonatkozó hatványa egyenlő, a két kör metszéspontjain átmenő egyenes, akkor megoldásunk rövidebben is befejezhető. A P pontnak a k körre vonatkozó hatványa BP⋅PC, a k' körre vonatkozó hatványa A1P⋅PD1, mivel ez a két szorzat az A1BD1C húrnégyszögben egyenlő, P ‐ és hasonló módon Q is ‐ rajta van a k és k' körök hatvány‐vonalán, így a két kör centrálisa merőleges PQ-ra, a tükrözés miatt átmegy M-en, és felezi a k kör PQ egyenesre eső húrját.