Kezdőlap


Feladat:	1966. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1966/december, 195 - 196. oldal		PDF \| MathML
Témakör(ök):	Háromszög-egyenlőtlenség alkalmazásai, Trigonometrikus függvények, OKTV
Hivatkozás(ok):	Feladatok: 1966/december: 1966. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az adott szakaszok közös kezdőpontja $O$ , végpontjaik egy bizonyos helyzetben $A$ , $B$ , $C$ , $D$ , a betűzést úgy választva, hogy $A B C D$ ne hurkolt négyszöget adjon.

2. ábra

Ennek területe, mint ismeretes (2. ábra)

\begin{matrix} t = \frac{1}{2} \cdot A C \cdot B D \cdot sin φ, \end{matrix}

(2)

ahol

φ

A C

és

A D

átlók által bezárt szög.
A szakaszok kölcsönös helyzetét változtatva mindig fennáll

\begin{matrix} A C \leq A O + O C, B D \leq B O + O D, (0 \leq) sin φ \leq 1, \end{matrix}

tehát

\begin{matrix} t \leq \frac{1}{2} (A O + O C) (B O + O D) . \end{matrix}

Itt az egyenlőség teljesül, (2) tényezői (egymástól függetlenül) elérik legnagyobb értéküket, ha az

O A

és

O C

, valamint

O B

és

O D

szakaszok egymás meghosszabbításába esnek ‐ más szóval, ha

O

A C

és

B D

átlók metszéspontjává válik ‐, és ha még

φ = 90^{\circ}

, vagyis az átlók merőlegesek egymásra. Ekkor

t

legnagyobb értéke csak a szakaszok hosszától és azok két párba rendezésétől függ.
A 4 szakasz 2 párba állítása háromféleképpen lehetséges, mert az elsőnek kiválasztott szakasz meghosszabbításába a további 3 bármelyikét állíthatjuk, és ezután mindig a maradó 2 szakasz alkotja a másik párt. Legyen a 4 szakasz hossza

p

q

r

s

úgy, hogy

p \geq q \geq r \geq s (> 0)

, így a kétszeres terület legnagyobb értéke a következő 3 szorzat valamelyike: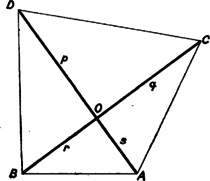

\begin{matrix} 2 t_{1} = (p + q) (r + s), 2 t_{2} = (p + r) (q + s), 2 t_{3} = (p + s) (q + r) . \end{matrix}

A harmadikból az elsőt, majd a másodikat kivonva a különbség így alakítható:

\begin{matrix} 2 (t_{3} - t_{1}) = (p - r) (q - s), 2 (t_{3} - t_{2}) = (p - q) (r - s) . \end{matrix}

Ezek egyike sem negatív, tehát

t_{3} \geq t_{1}

t_{3} \geq t_{2}

, így

p

-nek

s

-sel ‐ vagyis a leghosszabb szakasznak a legrövidebbel ‐ egy átlóba állítása esetén kapunk legnagyobb területű négyszöget (3. ábra).

3. ábra

II. megoldás. A fentebbi jelölésekkel az

O A B

O B C

O C D

és

O D A

háromszög területe külön-külön akkor a legnagyobb, ha

O

-ból kiinduló két oldaluk merőleges egymásra. Ez a 4 feltétel egyidejűen teljesíthető úgy, hogy a négy háromszög

O

-nál levő derékszögeivel kitöltjük az

O

pont körüli

360^{\circ}

-os szögtartományt, és ekkor az

A B C D

négyszög területe is a legnagyobb, egyenlő a négy derékszögű háromszög területének összegével. Ebben az elhelyezésben 2‐2 szakasz egymás meghosszabbításába esik, és az

A B C D

négyszög egy-egy átlóját alkotja.
A szakaszok fenti 3 párosításából akkor kapunk legnagyobb területet, ha az egyik átló a legkisebb és a legnagyobb szakasz összege. Ismeretes ugyanis, hagy két egyenlő kerületű téglalap közül annak nagyobb a területe, amelyikben az oldalak különbsége (abszolút értékben) kisebb. Más szóval, ha két (két-tényezős) szorzatban a tényezők összege ugyanakkora, akkor az a szorzat nagyobb, amelyikben a tényezők kevesebbel térnek el egymástól. Esetünkben a két tényező a 4 adott szakaszból alkotott két páros összeg, és ezek eltérése akkor a legkisebb, ha a legkisebb szakaszt a legnagyobbikkal állítjuk párba.