Kezdőlap


Feladat:	1966. évi Matematika OKTV I. forduló 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1966/december, 193 - 194. oldal		PDF \| MathML
Témakör(ök):	Trapézok, Thalesz-kör, Derékszögű háromszögek geometriája, OKTV
Hivatkozás(ok):	Feladatok: 1966/december: 1966. évi Matematika OKTV I. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megoldás. A megszerkesztendő $A B C D$ trapéz egyenlő szárú, mert húrtrapéz, és szárai a hosszabb párhuzamos oldal szemben levő végpontjából mindenesetre hegyes szögben látszanak, így kisebbek a kör átmérőjénél. A trapéznak a kör átmérőjével egyenlő $A B$ oldala tehát a hosszabb párhuzamos oldal.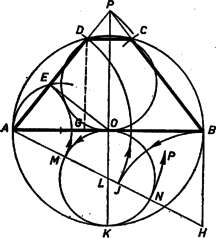

1. ábra

A szár hosszát számítással határozzuk meg. Legyen

A B = 1

A D = B C = x

D

vetülete az

A B

oldalon

G

(1. ábra). Az

A B D

háromszög Thalész tétele alapján derékszögű, így az ismert mértani középarányos tétel szerint

A D^{2} = A B \cdot A G

, azaz

A G = x^{2}

. Ezért

D C = A B - 2 A G = 1 - 2 x^{2}

. Mivel továbbá a trapézba kör írható, azért

A D + B C = A B + D C

, vagyis

\begin{matrix} 2 x = 1 + (1 - 2 x^{2}), \end{matrix}

(1)

aminek pozitív gyöke

\begin{matrix} x = \frac{\sqrt[]{5}}{2} - \frac{1}{2} . \end{matrix}

Ennek alapján a szerkesztés a következő. Az adott kör

O

középpontján át tetszés szerint felvett

A B

átmérő

B

végpontjában meghúzzuk az érintőt, felmérjük rá a

B H = B O = 1 / 2

szakaszt, ekkor

A H = \sqrt[]{5} / 2

. Az

A H

szakaszt metszük a

H

körül

H B

sugárral írt körrel

J

-ben, ekkor

A J = x

. Végül az

A

és

B

körül

A J

sugárral írt körívvel az adott körből kimetsszük a

D

, illetőleg

C

csúcsot.
Így a csúcsok a körön vannak, másrészt teljesül (1) is, ezért a trapézba érintő kör írható, tehát megfelel a követelményeknek.

Megjegyzés. A fenti szerkesztést felére kicsinyítve végezhetjük el, a kör

A B

-re merőleges sugarai egyike,

O K

fölé kört írva. Ennek középpontját

L

-lel,

A L

-lel való metszéspontjait

M

-mel és

N

-nel jelölve

(A M < A N) A M = A J / 2

, ennek alapján az

A O

átmérőjü Thalész körből kimetszhetjük az

A D

oldal

E

felezőpontját.
Az

N

metszéspont alapján viszont a szárak

P

metszéspontját jelölhetjük ki a trapéz szimmetriatengelyén. Ugyanis

O E

, mint az

O A D

egyenlő szárú háromszög magassága, merőleges

A P

-re, így a

P A O

derékszögű háromszögből

\begin{matrix} A P = \frac{A O^{2}}{A E} = \frac{1}{4 \cdot A E} = \frac{1}{4 \cdot A M} = \frac{1}{\sqrt[]{5} - 1} = \frac{\sqrt[]{5}}{4} + \frac{1}{4} = A L + L N = A N . \end{matrix}