Kezdőlap


Feladat:	1965. évi Matematika OKTV II. forduló 2. feladata	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1965/november, 106 - 110. oldal		PDF \| MathML
Témakör(ök):	Szögfelező egyenes, Trapézok, Beírt kör, OKTV
Hivatkozás(ok):	Feladatok: 1965/november: 1965. évi Matematika OKTV II. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $A B C$ háromszögbe írt négyzet $D$ és $E$ csúcsa legyen a $B C$ egyenesen, $F$ és $G$ pedig a $C A$ , illetőleg $A B$ egyenesen. Megmutatjuk, hogy a beírt kör középpontja nem lehet az $A F G$ , $B D G$ , $C E F$ háromszögek egyikében sem. Mivel a középpont a belső szögfelezők metszéspontja, állításunk könnyen adódik a következő segédtételből.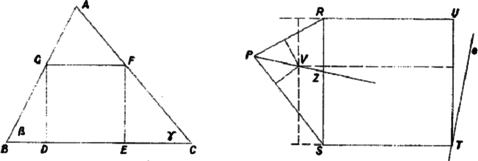

Ha egy

P R S

háromszög

R

-nél és

S

-nél levő szöge nem tompaszög, és az

R S

oldalra, annak ellenkező oldalán, mint amelyiken a háromszög van,

R S T U

négyzetet rajzolunk, továbbá a

T

csúcson át egy

e

egyenest húzunk, amelyik nem metszi a négyzetet, akkor az

R P S

szög felezőjének a háromszögbe eső minden

V

pontja messzebb van

e

-től, mint a

P R

P S

egyenesektől. A

P R U T S

ötszög a háromszög szögeire tett feltevés folytán konvex, így az egyenes teljesen rajta kívül fekszik, tehát

V

-t

e

bármely pontjával összekötő szakasz metszi az ötszög kerületét, tehát hosszabb valamelyik ötszögoldaltól való távolságnál. Ezek között viszont a

P R

P S

oldalaktól való (egyenlő) távolság a legkisebb, mert az

R U

S T

oldalakra bocsátott merőleges metszi

P R

-t, illetőleg

P S

-t, tehát hosszabb a megfelelő oldaltól való távolságnál, a

T U

oldaltól való távolság viszont nagyobb a négyzetoldalnál, míg a

P R

P S

-től való távolság nem nagyobb, mint a szögfelező és az

R S

oldal

Z

metszéspontjának távolsága ezektől az egyenesektől, az pedig nem nagyobb a

Z R

Z S

kisebbikénél, s így nem nagyobb a négyzetoldal felénél.
Segédtételünk alkalmazható az

A F G

B D G

C E F

háromszögekre, ha az

A B C ∢ = β

és

A C B ∢ = γ

nem tompaszög, mert ekkor az

A F G

háromszög

F

-nél és

G

-nél levő szöge

γ

, illetőleg

β

, tehát nem tompaszög. A

B D G

és

C E F

háromszög, ha nem válik egyenesszakasszá, akkor derékszögű, és a közös oldalnak ellenkező oldalán van, mint a négyzet. Így a beírt kör középpontja nem lehet a szögfelezőknek a négyzeten kívüli részében, tehát a négyzetbe kell hogy essék.

Megjegyzés. Csak a négyzetoldalak melletti szögekről használtuk ki hegyesszög voltukat, így ha a beírt négyzet két csúcsa a legnagyobb oldalon van, az állítás minden háromszögre érvényes. Az állítás érvényessége a további megoldások bizonyításaiból is adódik, a III. megoldás esetében a megjegyzésbeli kiegészítéssel.

II. megoldás. Az előző megoldás jelöléseit használva azt mutatjuk meg, hogy mindegyik szögfelező a négyzet két szemközti oldalát metszi. Ebből következik, hogy a

B

-ből, illetőleg

C

-ből húzott szögfelező a

C F

, illetőleg

B G

szakaszon metszi a szemközti oldalt, így mindkettőnek a háromszögbe eső szakasza benne van a

B C F G

trapézban, a harmadik szögfelezőnek a háromszögbe eső szakaszát viszont az

A G D E F

ötszög tartalmazza, így metszéspontjuk a mindkét idom által fedett síkrészben, tehát a

D E F G

négyzetben van.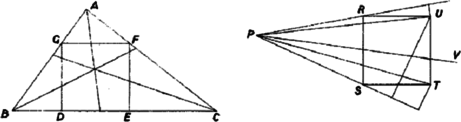

A három háromszög esetét ismét együtt tárgyalhatjuk. A

P R S

háromszög

R

-nél és

S

-nél levő szöge ne legyen tompaszög, rajzoljunk az

R S

oldalra, annak ellenkező oldalán, mint amelyiken a háromszög van,

R S T U

négyzetet, és az

R P S

szög felezőjének egy pontja legyen

V

. A feltételekből következik, hogy

U

és

T

R P S

szögtartományban van.
A szögfelező pontjai egyenlő távol vannak a

P R

és

P S

egyenestől, az

R P V

szögtartomány pontjai az

R P

szárhoz, az

S P V

tartományéi az

S P

szárhoz vannak közelebb. Az

U

pont távolsága a

P R

egyenestől kisebb

U R

-nél, tehát a négyzet oldalánál. Másrészt

U

R S T

szögtartományban van, tehát a belőle

P S

-re bocsátott merőleges metszi az

R S

vagy

S T

egyenest, s így már a négyzetbe eső szakasza legalább akkora, mint

U R

vagy

U T

, tehát mint a négyzet oldala. Így

U

R P V

szögtartományban van, és ugyanígy látható, hogy

T

S P V

szögtartományban van. Így a szögfelező az

U P T

szögtartományban van, tehát metszi az

U T

szakaszt, másrészt az

R S

szakaszt is, tehát a négyzet két átellenes oldalát. Ezt akartuk bizonyítani.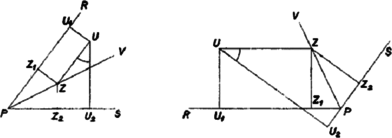

Megjegyzés. Felhasználtuk azt, hogy az

R P V

szögtartományban levő

U

pont közelebb van

R P

-hez, mint

S P

-hez. Ezt így láthatjuk be: Legyen

U

vetülete a

P R

, illetőleg

P S

egyenesen

U_{1}

, illetőleg

U_{2}

, az

U

-n át

P R

-rel párhuzamos egyenes metszéspontja a szögfelezővel

Z

, és ennek vetülete

P R

-en és

P S

-en

Z_{1}

és

Z_{2}

. Ekkor egyrészt az

U_{1} U Z Z_{1}

téglalapból, és mert

Z

a szögfelezőn van,

U U_{1} = Z Z_{1} = Z Z_{2}

. Másrészt az

U_{2} U Z ∢

hegyesszög (vagy

0^{\circ}

), mert vagy

U_{2} U

fut a derékszögű

U_{1} U Z

szögtartományban (ha

R P S ∢ > 90^{\circ}

), vagy az

U_{1} U U_{2}

szögtartomány tartalmazza

U Z

-t. Így az

U_{2} U Z Z_{2}

derékszögű trapézban (ami egyenesszakasszá is lapulhat)

U U_{2} > Z Z_{2} = Z Z_{1} = U U_{1}

, és ezt akartuk bizonyítani.

III. megoldás. Hegyesszögű háromszögre bizonyítjuk az állítást a feladat szövegének megfelelően, az előző megoldás segédtételére adva új bizonyítást, ha

R P S

szög hegyesszög.
Először azt az esetet vizsgáljuk, ha a háromszög

S

-nél derékszögű. Messe a

P

-ből húzott szögfelező az

R U

egyenest

V

-ben. A

P R V

háromszög egyenlő szárú, mert

R V P ∢ = V P S ∢ = V P R ∢

. Így

V R = P R > R S = R U

, vagyis

V

R U

oldal

U

-n túli meghosszabbításán van. A

P V

szakasz tehát az egymással szemben levő

S R

és

T U

oldalakat metszi.

R

-nél és

S

-nél hegyesszög van a

P R S

háromszögben, akkor rajzoljuk meg a háromszög köré írt kört. A

P

-ből húzott szögfelező ezt a

P

-t nem tartalmazó

S R

ív

Z

felezőpontjában metszi. Messe

U R

és

T S

meghosszabbítása a kört másodszor

P_{1}

-ben, illetőleg

P_{2}

-ben. Mivel a háromszög hegyesszögű,

P

a rövidebb

P_{1} P_{2}

íven van. Az

S P_{1} R ∢

és

S P_{2} R ∢

felező egyenese is átmegy

Z

-n, és az előbbi szerint közrefogja a

P Z

szögfelezőt. Az első két szögfelező a föntebb tárgyalt speciális esetből adódóan a

T U

szakaszt metszi, tehát a köztük levő

P Z

szögfelező is, és ezt akartuk bizonyítani.

Megjegyzés. Ha

S P R ∢ \geq 90^{\circ}

, akkor pl. abból adódik a segédtétel helyessége, hogy

Z

nincs messzebb

T U

-tól, mint

R S

-től, s így

P

rá vonatkozó

P'

tükörképe a

T U

ellenkező oldalán van, mint

P

, és azzal együtt az

R U

és

S T

egyenesek közt fekszik.

IV. megoldás. Mozgassunk egy

B C

-vel párhuzamos

e

egyenest a

B C

oldaltól

A

felé, és bocsássunk az

A B

és

A C

oldallal való

G

és

F

metszéspontból minden helyzetben merőlegest

B C

-re. A keletkező beírt téglalap

F G

oldala a rá merőleges oldal növekedésével állandóan csökken.
Amig

e

elválasztja a beírt kör

O

középpontját és a

B C

oldalt, addig a téglalap magassága legfeljebb a beírt kör

ϱ

sugarát érheti el, viszont alapja nem kisebb az

O

-n átmenő egyenes háromszögbe eső szakaszánál, ami nagyobb

2 ϱ

-nál. A beírt négyzet tehát ezek közt a téglalapok közt nem szerepel.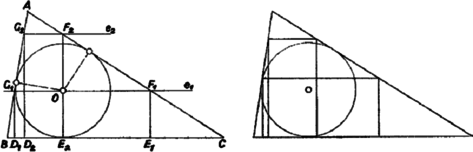

Tovább mozgatva

e

-t, a téglalapok mindaddig tartalmazzák

O

-t, míg az az egyik

B C

-re merőleges oldalra nem kerül. Tartozzék ehhez a helyzethez a

D_{2} E_{2} F_{2} G_{2}

téglalap, és essék

O

pl. az

E_{2} F_{2}

oldalra. Ekkor

E_{2} F_{2} > 2 ϱ

, viszont

G_{2} F_{2} \leq ϱ

, ugyanis az

A B

és

A C

oldalak érintkezési pontja a körrel az

A G_{2}

, ill.

A F_{2}

szakaszok meghosszabbításán van (hiszen közelebb van

B C

-hez, mint

2 ϱ

), a

G_{2} D_{2}

egyenes pedig a

B A C

szögtartományban halad, ha

A B C

szög és

A C B

szög nem tompa, így van közös pontja a körrel, tehát annak

E_{2} F_{2}

-re merőleges sugarával is. Így ez a téglalap sem négyzet, sem azok, amelyek

e

-nek

A

felé történő továbbmozgatásával keletkeznek.
Az

A B C

háromszögbe beírt,

B C

oldalon nyugvó négyzetnek ezek szerint az

O

-t belsejükben tartalmazó téglalapok közt kell lennie.

Megjegyzés. A többi megoldásból is kiolvasható, amit itt kimondtunk, hogy a négyzet a kör középpontját belsejében tartalmazza.
Az utolsó megoldás azt is adja, hogy a háromszögbe beírt fél-négyzetek ‐ akár a

B C

-n nyugvó oldal fele a másiknak, akár a rá merőleges oldal ‐ szintén belsejükben tartalmazzák a beírt kör középpontját. Ez könnyen leolvasható az első megoldásból is.