Feladat:	1965. évi Matematika OKTV II. forduló 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1965/november, 104 - 106. oldal		PDF  |  MathML
Témakör(ök):	Trigonometriai azonosságok, Másodfokú (és arra visszavezethető) egyenletrendszerek, Középponti és kerületi szögek, Síkgeometriai számítások trigonometria nélkül háromszögekben, OKTV
Hivatkozás(ok):	Feladatok: 1965/november: 1965. évi Matematika OKTV II. forduló 1. feladata

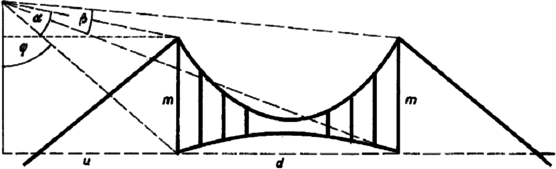
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.     I. megoldás. Legyen a keresett magasság${}^{*}$ $h$, a megfigyelő szemének merőleges vetülete a feladatban szereplő síkon legyen $u$ távolságra a budai kapuzattól ‐ jelöljük ennek látószögét $\alpha$-val ‐ és az ennek alsó végpontjához vezető látósugár zárjon be $\phi$ szöget a függőleges iránnyal. Ekkor ${\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{tg}\phi }& {\displaystyle =\frac{u}{h}}\hfill \\ \hfill {\displaystyle \text{tg}\left(\phi +\alpha \right)}& {\displaystyle =\frac{u}{h-m}=\frac{\text{tg}\phi +\text{tg}\alpha }{1-\text{tg}\phi \text{tg}\alpha }=\frac{u/h+\text{tg}\alpha }{1-\left(u\text{tg}\alpha \right)/h}=\frac{u+h\text{tg}\alpha }{h-u\text{tg}\alpha }\mathrm{.}}\hfill \end{array}}$ Ebből $u$-ra és $h$-ra a következő egyenlet adódik: $\begin{array}{c}{\displaystyle uh-u^2\text{tg}\alpha =uh+h^2\text{tg}\alpha -um-hm\text{tg}\alpha \mathrm{,}}\end{array}$ vagy rendezve és cotg $\alpha$-val szorozva $\begin{array}{c}{\displaystyle u^2+h^2-um\text{ cotg }\alpha -hm=0.}\end{array}$ A pesti kapuzatra vonatkozóan ugyanilyen egyenlet adódik, csak $\alpha$ és $u$ helyébe $\beta$ és $u+d$ lép: $\begin{array}{c}{\displaystyle {\left(u+d\right)}^2+h^2-\left(u+d\right)m\text{ cotg }\beta -hm=0.}\end{array}$ A két egyenlet különbségét képezve meghatározható $u$ és ezt ismerve az első egyenletből a keresett $h$ magasság, mint az egyenlet pozitív gyöke: ${\displaystyle \begin{array}{c}\hfill {\displaystyle {\left(u+d\right)}^2-u^2-\left[u\left(\text{cotg }\beta -\text{cotg }\alpha \right)+d\text{ cotg }\beta \right]m=}\hfill \\ \hfill {\displaystyle =u\left[2d-m\left(\text{cotg }\beta -\text{cotg }\alpha \right)\right]-d\left(m\text{ cotg }\beta -d\right)=\mathrm{0,}}\hfill \\ \hfill {\displaystyle u=\frac{d\left(m\text{ cotg }\beta -d\right)}{2d-m\left(\text{cotg }\beta -\text{cotg }\alpha \right)}\mathrm{,}}\hfill \\ \hfill {\displaystyle h=\frac{m}{2}+\sqrt[]{\frac{m^2}{4}+um\text{ cotg }\alpha -u^2}\mathrm{.}}\hfill \end{array}}$ Adataink közül csak a nagyobbik szög lehet a budai és a kisebb a pesti kapuzat látószöge, mert megcserélve a szögeket $m\cdot \text{cotg }11\mathrm{,}{4}^{\circ }<40\cdot 5=200$ folytán $u$-ra negatív értéket kapnánk. A számításokat $4$ jegyű függvénytáblázattal végezve ${\displaystyle \begin{array}{c}\hfill {\displaystyle m\text{ cotg }\beta =196\mathrm{,}\mathrm{4,}m\left(\text{cotg }\beta -\text{cotg }\alpha \right)=\mathrm{288,}}\hfill \\ \hfill {\displaystyle 2d-m\left(\text{cotg }\beta -\text{cotg }\alpha \right)=\mathrm{292,}}\hfill \\ \hfill {\displaystyle \text{lg}u=2\mathrm{,}\mathrm{2902,}um\text{ cotg }\alpha =38\mathrm{700,}}\hfill \\ \hfill {\displaystyle {\left(m/2\right)}^2=\mathrm{400,}{u}^2=38\mathrm{050,}}\hfill \\ \hfill {\displaystyle h=20+\sqrt[]{1050}=52\mathrm{,}4\approx 52\text{ m}\mathrm{.}}\hfill \end{array}}$ (Mivel az adatok egy része csak $2$ értékes jegyig ismert, az eredménynek is legfeljebb két jegye elfogadható.)     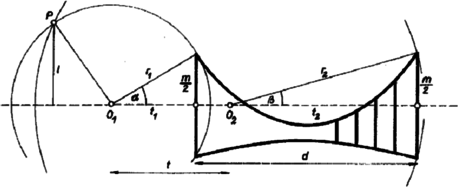II. megoldás. A megfigyelő $P$ nézőpontja egyrészt rajta van azon a látószögköríven; amelyről a közelebbi kapuzat $\alpha$ szög alatt látszik, másrészt azon is, amelyikről a távolabbi $\beta$ szög alatt látszik. Legyen a körök középpontja $O_1$, $O_2$, távolságuk a megfelelő kapuzattól $t_1$, ill. $t_2$, sugaruk $r_1$, ill $r_2$, $P$ távolsága az $O_1{O}_2$ egyenestől $l$; ekkor a keresett magasság $m/2+l$. $l$-et mint az $O_1{O}_{2}P$ háromszög magasságát határozzuk meg. Az oldalak kiszámíthatók: $O_{1}P=r_1$, $O_{2}P=r_2$, és $O_1{O}_2=t_1+d-t_2$; jelöljük az utóbbit $t$-vel. A középponti és kerületi szögek közti összefüggésből adódik, hogy $r_1$, $t_1$ és $m/2$ egy $\alpha$ hegyesszöget tartalmazó derékszögű háromszög oldalai, $r_2$, $t_2$ és $m/2$ pedig egy $\beta$ hegyesszöget tartalmazóé, így ${\displaystyle \begin{array}{c}\hfill {\displaystyle r_1=\frac{m}{2\text{sin}\alpha }\mathrm{,}{r}_2=\frac{m}{2\text{sin}\beta }\mathrm{,}}\hfill \\ \hfill {\displaystyle t_1=\frac{m}{2}\text{ cotg }\alpha \mathrm{,}{t}_2=\frac{m}{2}\text{ cotg }\beta \mathrm{,}t=d+t_1-t_2\mathrm{.}}\hfill \end{array}}$ Mostmár a háromszög területét egyrészt az $l$ magasság felhasználásával, másrészt Heron képletével kiszámítva és $l$-et kifejezve ‐ ha $\left(r_1+r_2+t\right)/2$-t $s$-sel jelöljük ‐ $\begin{array}{c}{\displaystyle l=\frac{2\sqrt[]{s\left(s-r_1\right)\left(s-r_2\right)\left(s-t\right)}}{t}\mathrm{.}}\end{array}$ $4$ jegyű függvénytáblázatot használva $r_1=101\mathrm{,}2$, $r_2=244\mathrm{,}1$, $t=146$, $l=31\mathrm{,}5$ adódik, így $h=51\mathrm{,}5\approx 52$ m.   Megjegyzés. Adataink mellett $s-r_2=1\mathrm{,}5$ adódik, tehát a számított $4$-jegyű értékek utolsó két jegye játszik lényeges szerepet. Ebből érthető az eredmény pontatlansága, a két megoldásban kapott értékek eltérése. ${}^{*}$Az ábrán $h$ bejegyzése pótlandó.