Feladat: 1965. évi Matematika OKTV I. forduló 3. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1965/november, 101 - 104. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Magasságvonal, Húrnégyszögek, Háromszögek egybevágósága, Háromszögek hasonlósága, Pont körüli forgatás, Középponti és kerületi szögek, Thalesz-kör, Indirekt bizonyítási mód, OKTV
Hivatkozás(ok):Feladatok: 1965/november: 1965. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az alábbi megoldások mindegyikében a kört az ABC háromszög AB oldala, mint átmérő fölé rajzoljuk. A háromszögekben szokásos jelöléseket használjuk, legyen továbbá a kör és az AC, BC oldal metszéspontja P, illetőleg Q, a kör középpontja O, és a háromszög magasságpontja 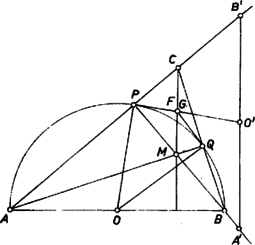M.

 
I. megoldás. Messe a CM magasságvonalat a kör P-beli érintője F-ben, a Q-beli érintő G-ben (2. ábra). Azt kell belátnunk, hogy F és G egybeesnek.
 
 
2. ábra
 

Thalész tétele miatt P a B-ből húzott magasság talppontja, ezért a P körüli, pozitív irányú 90∘-os elforgatás az ABP háromszöget átviszi egy a hozzá hasonló MCP háromszöggel párhuzamos oldalú háromszögbe, a PO sugarat pedig a rá merőleges PF érintőre. Mivel O felezi AB-t, azért F a CM szakasz felezőpontja. Az ABQ háromszöget Q körül az előbbivel ellentétes irányban átforgatva a CMQ háromszöggel hasonló helyzetbe, ugyanígy látható, hogy G is a CM szakasz felezőpontja, azaz egybeesik F-fel. ‐ Ezzel a feladat állításánál többet bizonyítottunk be, mégpedig azt, hogy a kérdéses metszéspont felezi a magasságpont és az első oldallal szemben fekvő csúcs közti szakaszt.
 
II. megoldás. Megmutatjuk, hogy a P és Q pontokban húzott érintők H metszéspontját C-vel összekötő egyenes merőleges AB-re, vagyis az ABC háromszög magasságvonala.
A HPQ háromszög egyenlő szárú; P-nél és Q-nál levő szöge egyenlő a kör PQ ívéhez tartozó bármely kerületi szöggel, így a PBQ szöggel is, melynek nagysága a PBC derékszögű háromszögből 90∘-y. Ezért a PQ szakasz H-ból 180∘-2(90∘-y)=2y szögben látszik. PQ-nak C-ből vett látószöge viszont y, és mivel C és H a PQ egyenesnek ugyanazon a partján van, azért a H körül írt, P-n és Q-n átmenő kör átmegy a C csúcson is. Ezért a CHQ háromszög egyenlő szárú, tehát
HQC∢=QCH∢=BCT∢,(1)
ahol T az AB és CH egyenesek metszéspontja.
A HQC szög csúcsszöge egy a QB íven nyugvó kerületi szög, ezért egyenlő az ugyanazon az íven nyugvó QAB szöggel, ami 90∘-β. Így a BCT háromszög C-nél levő szöge 90∘-β, vagyis a B-nél levő szögének pótszöge, ezért a T-nél levő szöge derékszög, CT vagyis CH valóban merőleges 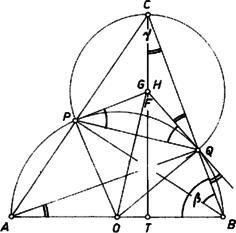AB-re.
 
 
3. ábra
 

III. megoldás. A C-ből húzott magasság és a Q pontbeli érintő metszéspontját ismét G-vel jelölve azt fogjuk megmutatni, hogy a G mint középpont körül írt, C-n áthaladó körön rajta van P is, Q is (3. ábra). Ebből ugyanis már következik, hogy GP=GQ, és így az OPG és OQG háromszögek három-három oldalban megegyezve egybevágóak, ezért a GPO szög egyenlő a GQO szöggel, az utóbbi pedig 90∘, tehát GP a P-ben húzott körérintő.
Az AOQ és CGQ háromszögek oldalai páronként merőlegesek egymásra, tehát a háromszögek hasonlóak, és így az előbbivel együtt az utóbbi is egyenlő szárú háromszög, QG=CG, Q valóban a mondott körön van, és
CGQ∢=AOQ∢=2ABQ∢,
mert az utolsó két szög az AQ íven nyugvó középponti, illetőleg kerületi szög.
Másrészt az ABQP húrnégyszögben az ABQ belső és a CPQ külső szög egyenlő, mert mindkettő az APQ szög 180∘-ra kiegészítő szöge, ezért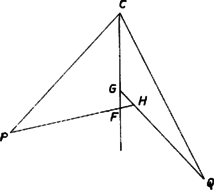
CGQ∢=2CPQ∢.
Végül G és P a BC oldalegyenes ugyanazon oldalán van, ezért a mondott kör átmegy a P ponton is. Ezt akartuk bizonyítani.
 
IV. megoldás. Legyen a C-ből húzható magasság és a P-beli, illetőleg Q-beli érintő metszéspontja ismét F, illetőleg G, a két érintő metszéspontja H. Az előző megoldásban láttuk, hogy CG=QG. Hasonlóan látható be, hogy CF=PF. Továbbá PH=QH, mert a körhöz a H pontból húzható érintőszakaszok.
 
 
4. ábra
 

Ha F, G és H nem esne egybe, és például G a CF szakasz belső pontja lenne (4. ábra), akkor H a PF szakasz F-en túli meghosszabbításán és a QG szakasz belsejében lenne, mert így (és az eredeti feltevések szerint) PF belső pontban metszi a CGQ háromszög CQ oldalát, a CG oldalát viszont a meghosszabbításán, tehát a GQ oldalt is belső pontban metszi, vagyis
PH>PF=CF>CG=QG>QH=PH,
ami lehetetlen.
Ha F esnék a CG szakaszra, akkor hasonlóan adódik, hogy mindenütt az ellenkező értelmű egyenlőtlenség állana fenn, ami ugyancsak lehetetlen. Kell tehát, hogy a három pont egybeessék, és így az érintők a magasságvonalon messék egymást.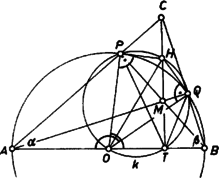
 
 
5. ábra
 

V. megoldás. Legyen a két érintő metszéspontja H, a C csúcsból húzott magasság talppontja T (5. ábra). Említettük már, hogy AQ és BP a háromszög másik két magassága. OHP és OHQ háromszögek derékszögűek, és az OH szakasz mint átmérő fölé rajzolt k kör átmegy P-n és Q-n. Megmutatjuk. hogy ez a kör átmegy a T talpponton is1. Ebből már következik a feladat állítása, ugyanis ekkor az OTC derékszög TC szára átmegy az O-ból induló átmérő másik végpontján, a H ponton is.
Az AOQ és a BOP szög, mint a BOQ, illetőleg AOP egyenlő szárú háromszög külső szöge, 2β, illetve 2α nagyságú, másrészt együttesen a 180∘-ot egyszer és a POQ szöget kétszeresen fedik le, így
POQ∢=2α+2β-180∘=180∘-2y.

Az ATQC és BTPC négyszögek húrnégyszögek (az első az AC, a második a BC mint átmérő fölé rajzolt Thalesz-körben), és így a BTQ, illetőleg ATP külső szögük egyenlő a PCQ=y szöggel. Ezek alapján
PTQ∢=180∘-ATP∢-BTQ∢=180∘-2y=POQ∢.

Mivel O és T a PQ egyenesnek ugyanazon az oldalán fekszik, azért O, P, Q és T valóban egy körön van, és ezzel igazoltuk állításunkat.
 

Megjegyzések. 1. A feladat megoldható a koordinátageometria módszereivel is, de így még a koordinátarendszer szokásos célszerű megválasztása esetén is hosszadalmas számításokkal jutunk célhoz.
2. Ha az ABC háromszög bármelyik szöge derékszög, a feladat állítása érdektelen. Ha ugyanis a derékszög C-nél van, a kérdéses érintők, ha pedig A és B valamelyikénél van, akkor az egyik érintő és a magasság esik egybe.
3. Az olvasó a fenti megoldások csekély változtatásával könnyen beláthatja, hogy az állítás tompaszögű háromszögre is igaz, oldalszakasz helyett természetesen oldalegyenest mondva. Egy ilyen helyzetet mutat be a 6. ábra.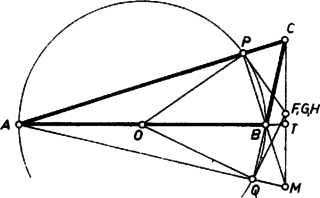
 
 
6. ábra
 
1A k kör az ABC háromszög Feuerbach-köre, amely átmegy a magasságok talppontjain, az oldalak felezőpontjain és a magasságpontot a csúcsokkal összekötő szakaszok felezőpontjain. Lásd pl. Gallai T.‐ Hódi E. ‐ Péter R. ‐ Szabó P. ‐ Tolnai J.: Matematika az ált. gimn. III. o. számára, 12. kiadás, Tankönyvkiadó, Bp. 1962. 183 ‐ 188. o. ‐ Az alábbiakban azonban erre való hivatkozás nélkül bizonyítjuk be állításunkat.