Kezdőlap


Feladat:	1964. évi Matematika OKTV II. forduló 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1964/november, 105 - 107. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szögfüggvények, síkgeometriai számítások, Koszinusztétel alkalmazása, OKTV
Hivatkozás(ok):	Feladatok: 1964/november: 1964. évi Matematika OKTV II. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Írjunk $γ$ helyébe $180^{\circ} - (α + β)$ -t, majd igyekezzünk szorzattá alakítani:

\begin{matrix} cos α + cos β + cos γ = cos α + cos β - cos α cos β + sin α sin β = \\ = cos α + (1 - cos α) cos β + sin α sin β = \\ = 1 - (1 - cos α) + (1 - cos α) cos β + sin α sin β = \\ = 1 - (1 - cos α) (1 - cos β) + sin α sin β . \end{matrix}

Itt a második tag nem pozitív, mert a koszinusz-függvény nem vesz fel

1

-nél nagyobb értéket, a harmadik pedig kisebb

1

-nél, mert egyik tényezője sem nagyobb

1

-nél, de nem lehet mindkettő egyszerre

1

sem (nem lehet

α

is,

β

90^{\circ}

). Így

\begin{matrix} cos α + cos β + cos γ < 2, \end{matrix}

és ezt akartuk bizonyítani.

II. megoldás. Az állítás helyes, ha a háromszög nem hegyesszögű, mert ekkor az egyik tag nem pozitív, a másik kettő mindegyike pedig

1

-nél kisebb.
Hegyesszögű háromszögben válasszuk a betűzést úgy, hogy

γ

és a vele szemben levő

A B = c

oldal legyen a legkisebb, illetve a legkisebbek egyike. Jelöljük továbbá

γ

csúcsát

C

-vel, az

A C

B C

oldalakat

b

-vel, ill.

a

-val; legyen

C

merőleges vetülete az

A B

egyenesen

C_{1}

, ez az oldal belső pontja. Így

\begin{matrix} c = A C_{1} + C_{1} B = b cos α + a cos β . \end{matrix}

Innen, mivel feltevés szerint

a ≧ c

b ≧ c

, így

\begin{matrix} 1 = \frac{b}{c} cos α + \frac{a}{c} cos β \geq cos α + cos β; \end{matrix}

a harmadik szögre

cos γ < 1

, tehát helyes az állítás hegyesszögű háromszögben is.

III. megoldás. A bizonyítandó egyenlőtlenség, mint az előző megoldásban is láttuk, nyilvánvalóan helyes, ha a háromszög nem hegyesszögű. Hegyesszögű háromszögre

α_{1} = 90^{\circ} - α

β_{1} = 90^{\circ} - β

γ_{1} = 90^{\circ} - γ

pozitív hegyesszögek, melyek összege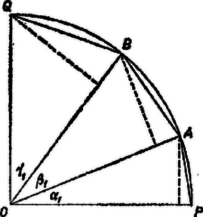

90^{\circ}

, és

\begin{matrix} cos α + cos β + cos γ = sin α_{1} + sin β_{1} + sin γ_{1} . \end{matrix}

Ezt az összeget szemléltethetjük a következő módon: egységnyi sugarú

O P Q

negyedkörbe rajzoljuk be az

α_{1}

, ill.

β_{1}

nagyságú

P O A

A O B

szögeket (1. ábra).

1. ábra

Ekkor

B O Q ∢ = γ_{1}

, és a

P O A

A O B

B O Q

háromszögekben a sugár alkotta oldalakra merőleges magasság hossza rendre

sin α_{1}

sin β_{1}

sin γ_{1}

, így a vizsgálandó összeg az

O P A B Q

ötszög területének kétszeresével egyenlő, tehát kisebb, mint az egységnyi sugarú félkör területe,

π / 2

. Hegyesszögű háromszögre tehát

\begin{matrix} cos α + cos β + cos γ < \frac{π}{2} (< 1, 571) . \end{matrix}

IV. megoldás. Alakítsuk két koszinusz összegét szorzattá:

\begin{matrix} cos β + cos γ = 2 cos \frac{β + γ}{2} cos \frac{β - γ}{2} = 2 sin \frac{α}{2} cos \frac{β - γ}{2} \leq 2 sin \frac{α}{2}, \end{matrix}

mert mindkét tényező pozitív, hiszen

α / 2

és

| β - γ | / 2

hegyesszögek. Fejezzük ki

cos α

-t is a fele akkora szög szinuszával, akkor azt nyerjük, hogy

\begin{matrix} cos α + cos β + cos γ \leq 1 - 2 sin^{2} \frac{α}{2} + 2 sin \frac{α}{2} = \frac{3}{2} - \frac{1}{2} {(1 - 2 sin \frac{α}{2})}^{2} . \end{matrix}

A második tag nem lehet pozitív, így a bizonyítandó állításon túlmenően azt bizonyítottuk be, hogy

\begin{matrix} cos α + cos β + cos γ \leq \frac{3}{2} . \end{matrix}

(1)

Itt akkor érvényes az egyenlőség jele, ha egyrészt

cos ((β - γ) / 2) = 1

, másrészt

sin (α / 2) = 1 / 2

. Az első egy háromszög szögeire csak akkor teljesül, ha

β = γ

, a második akkor, ha

α = 60^{\circ}

; ekkor az első feltétel szerint

β = γ = 60^{\circ}

, azaz a háromszög szabályos.
Az (1) egyenlőtlenségben tehát szabályos háromszögre egyenlőség, más háromszögekre a ,,kisebb'' jel érvényes.

Megjegyzés. Az előző megoldás ábrája alapján finomabb elemzéssel szintén bizonyítható az (1) egyenlőtlenség hegyesszögű háromszögre, és kiterjeszthető a meggondolás nem hegyesszögű háromszögekre is.

V. megoldás. Fejezzük ki a szögek koszinuszát a koszinusz-tétel alapján az oldalakkal. Vizsgáljuk először két koszinusz összegét:

\begin{matrix} cos α + cos β = \frac{- a^{2} + b^{2} + c^{2}}{2 b c} + \frac{a^{2} - b^{2} + c^{2}}{2 a c} = \\ = \frac{a^{2} - b^{2}}{2 c} (\frac{1}{a} - \frac{1}{b}) + \frac{c}{2} (\frac{1}{a} + \frac{1}{b}) = \frac{1}{2} (\frac{c}{a} + \frac{c}{b}) - \frac{(a + b) {(a - b)}^{2}}{2 a b c} . \end{matrix}

Mindhárom szögpárra felírva a megfelelő kifejezést és összeadva azokat, a pozitív tagok összegében fellép miden törttel a reciproka is, így az összeg a következőképpen alakítható tovább:

\begin{matrix} 2 (cos α + cos β + cos γ) = \frac{1}{2} (\frac{a}{b} + \frac{b}{a} + \frac{b}{c} + \frac{c}{b} + \frac{c}{a} + \frac{a}{c}) - \\ - \frac{(a + b) {(a - b)}^{2} + (b + c) {(b - c)}^{2} + (c + a) {(c - a)}^{2}}{2 a b c} = \\ = 3 + \frac{1}{2} (\frac{{(a - b)}^{2}}{a b} + \frac{{(b - c)}^{2}}{b c} + \frac{{(c - a)}^{2}}{a c}) - \\ - \frac{(a + b) {(a - b)}^{2} + (b + c) {(b - c)}^{2} + (c + a) {(c - a)}^{2}}{2 a b c} = 3 - \\ - \frac{(a + b - c) {(a - b)}^{2} + (b + c - a) {(b - c)}^{2} + (c + a - b) {(c - a)}^{2}}{2 a b c} \leq 3, \end{matrix}

ugyanis mindegyik négyzet szorzója pozitív, mert a háromszög két oldalának az összege nagyobb, mint a harmadik oldal. Így

\begin{matrix} cos α + cos β + cos γ \leq \frac{3}{2} . \end{matrix}

(1)

Itt akkor áll egyenlőség, ha a fenti tört számlálójában

a - b = b - c = c - a = 0

, azaz szabályos háromszögre.

Megjegyzés: többen észrevették a bal oldal következő átalakítási lehetőségét:

\begin{matrix} \frac{a^{2} b + a^{2} c + a b^{2} + b^{2} c + a c^{2} + b c^{2} - a^{3} - b^{3} - c^{3}}{2 a b c} = \\ = \frac{(a + b - c) (a - b + c) (- a + b + c) + 2 a b c}{2 a b c} . \end{matrix}

Innen Heron képletét, az

a b c = 4 r t

és

t = ϱ s

összefüggéseket felhasználva, ahol

s

a kerület felét,

t

a háromszög területét,

r

és

ϱ

a körülírt és beírt kör sugarát jelöli, a következőt nyerjük:

\begin{matrix} cos α + cos β + cos γ = 1 + \frac{16 t^{2}}{16 r t s} = 1 + \frac{ϱ}{r} . \end{matrix}

Világos, hogy

ϱ < r

, amiből következik a feladat állítása. Az is belátható (trigonometria felhasználása nélkül is), hogy

ϱ \leq r / 2

, amiből (1) következik.