Kezdőlap


Feladat:	1964. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1964/november, 101 - 104. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Középponti és kerületi szögek, OKTV
Hivatkozás(ok):	Feladatok: 1964/november: 1964. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen egy a $Q$ ponton áthaladó, a $B C$ -től különböző egyenesnek az $A B$ szárral való metszéspontja $E$ , $A C$ -vel való metszéspontja $F$ (8. ábra). A $P$ -ből az $E F$ -re húzott merőleges talppontja legyen 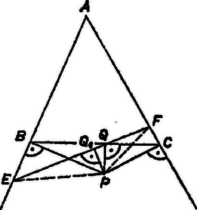$Q_{1}$ .

8. ábra

Hasonlítsuk össze (Pythagoras tétele alapján) a

B Q

és

E Q_{1}

, továbbá a

Q C

és

Q_{1} F

szakaszokat. A

B P Q

és

E P Q_{1}

derékszögű háromszögekből

\begin{matrix} B Q = \sqrt[]{B P^{2} - P Q^{2}}, E Q_{1} = \sqrt[]{E P^{2} - P Q_{1}^{2}} . \end{matrix}

P Q Q_{1}

és

P E B

derékszögű háromszögekből nyilvánvalóan

\begin{matrix} P Q > P Q_{1} \end{matrix}

(6)

\begin{matrix} és E P > B P . \end{matrix}

(7)

Ezek szerint

B Q

kifejezésében a kisebbítendő kisebb, a kivonandó pedig nagyobb, mint

E Q_{1}

kifejezésében, tehát

\begin{matrix} B Q < E Q_{1} . \end{matrix}

(8)

Ugyanígy a

P F C

derékszögű háromszögből adódó

\begin{matrix} P F > P C \end{matrix}

(9)

felhasználásával a

C P Q

F P Q_{1}

és

P Q Q_{1}

derékszögű háromszögekből

\begin{matrix} Q C = \sqrt[]{P C^{2} - P Q^{2}} < \sqrt[]{P F^{2} - P Q^{2}} < \sqrt[]{P F^{2} - P Q_{1}^{2}} = Q_{1} F . \end{matrix}

(10)

Megmutatjuk még, hogy

Q

B C

szakaszon,

Q_{1}

E F

szakaszon van. Ekkor (8)-at és (10)-et összeadva következik a bizonyítandó egyenlőtlenség:

\begin{matrix} B C = B Q + Q C < E Q_{1} + Q_{1} F = E F . \end{matrix}

(11)

Q

és

Q_{1}

helyzetére kimondott állítás így látható be. Az

A B C

háromszög

B

-nél és

C

-nél levő szöge hegyesszög, így az

A B

-re

B

-ben és

A C

-re

C

-ben állított merőlegeseknek az oldalegyenesektől a háromszöget tartalmazó félsíkba induló félegyenesei

B C

-vel hegyesszöget zárnak be. Így

P

ezeknek a félegyeneseknek a metszéspontja, vetülete,

Q

, a

B C

szakaszon van, és

P

B C

egyenes ellenkező oldalán fekszik, mint

A

.
Ha

E

A B

oldal

B

-n túli meghosszabbításán van ‐ amit a továbbiakban mindig felteszünk, mert, ha kell, a betűzés megcserélésével elérhetünk ‐, akkor

E

és

P

B C

egyenes ugyanazon oldalán van, tehát

B E P Q

konvex négyszög;

E

-nél levő szöge, mint a

B E P

derékszögű háromszög egyik szöge, hegyesszög,

Q

-nál levő szöge pedig derékszög, tehát az

E Q

átló

P E

-vel is,

P Q

-val is hegyesszöget zár be, s így

Q_{1}

E Q

szakasz belső pontja. Ezzel a bizonyítást befejeztük.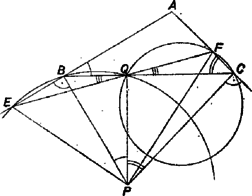

Megjegyzés. A feladat állítása érvényes, akármekkora is a háromszög

A

-nál levő szöge, hiszen csak a

B

és

C

csúcsnál levő szögről használtuk fel, hogy hegyesszögek. Világos, hogy érvényes marad akkor is, ha pl.

B

-nél derékszög van, ekkor ugyanis

P

és

Q

egybeesik

C

-vel. Ha viszont pl.

B

-nél tompaszög van, akkor a (11) egyenlőtlenség nem következik (8)-ból és (9)-ből, mert az utolsó két bekezdés meggondolásai nem érvényesek,

Q

B C

szakaszon kívül keletkezik, és valóban

E F

lehet kisebb is, nagyobb is, mint

B C

II. megoldás. Az I. megoldás (7) és (9) egyenlőtlensége szerint az

E P F

háromszögben a

P

-ből induló oldalak nagyobbak, mint a

B P C

háromszög megfelelő oldalai. Megmutatjuk, hogy egyrészt

E P F ∢ > B P C ∢

, másrészt hogy ebből, továbbá a

B C P

és

C B P

szögek hegyesszög voltából következik, hogy a harmadik oldal is az

E P F

háromszögben nagyobb.

9. ábra

A szögekre kimondott egyenlőtlenség igazolására rajzoljuk meg a

B

E

Q

, valamint a

C

F

Q

pontokon áthaladó köröket (9. ábra).

P

az első kör belsejében van, mert a

B Q

szakasz

P

-ből az

A B C

szöggel egyenlő szög alatt látszik (merőleges szárú hegyesszögek),

E

-ből pedig ennél kisebb szög alatt. A másik körön viszont kívül fekszik

P

, mert a

Q F C

ív

P

-ből vett látószöge akkora, mint az

A C B

szög, a

P

-vel egy oldalon levő kiegészítő ív pontjaiból vett látószög pedig nagyobb, mert innen a

Q F

rész-ív látható ekkora szög alatt. Ezek alapján

\begin{matrix} E P B ∢ > E Q B ∢ = F Q C ∢ > F P C ∢, \end{matrix}

és a két szélső szöghöz a

B P F

szöget hozzáadva valóban

\begin{matrix} E P F ∢ > B P C ∢ . \end{matrix}

(12)

10. ábra

E P F

és

B P C

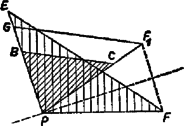háromszögek

E F

és

B C

oldalaira vonatkozó állítás igazolásához úgy forgattuk el a

B P C

háromszöget

P

körül, hogy

B

P E

szakaszra essék (10. ábra), a

P C

-nél hosszabb

P F

oldalt pedig

P

-től rámértük a

P C

félegyenesre is, a végpont

F_{1}

. Húzzunk most

B C

-vel párhuzamost

E

és

F_{1}

közül azon a ponton át, amelyik közelebb van

B C

-hez (a 10. ábrán az

F_{1}

pont az), messe a párhuzamos

P E

-t

G

-ben. Mivel

P C < P F = P F_{1}

, azért nyilvánvalóan

\begin{matrix} B C < G F_{1} . \end{matrix}

(13)

Ha az

A B C

háromszög

B

-nél és

C

-nél levő szöge hegyesszög, akkor a

P B C

-vel egyenlő

P G F_{1}

szög is hegyesszög, és így kiegészítő szöge, az

E G F_{1}

szög, tompaszög. Ezért

\begin{matrix} G F_{1} < E F_{1} . \end{matrix}

Ezt (13)-mal egybevetve

\begin{matrix} B C < E F_{1} . \end{matrix}

(14)

Mivel az

E P F_{1}

és

E P F

háromszögek két-két oldala egyenlő, de közbezárt szögük az előbbi háromszögben kisebb, azért¹

\begin{matrix} E F_{1} < E F, \end{matrix}

és ezt (14)-gyel egybevetve

B C < E F

; az állítást bebizonyítottuk.

Megjegyzés: A (12) egyenlőtlenség a következőképpen is belátható. Rajzoljunk köröket a

B P

és

C P

szakaszok, mint átmérők fölé; ezek egymást

P

-ben és

Q

-ban metszik. Legyen ezek

Q

-tól különböző metszéspontja

E F

-fel

E_{1}

, illetőleg

F_{1}

(11. ábra).

P

-ből az

E_{1} F_{1}

szakasz ugyanakkora szögben látható, mint a

B C

szakasz:

E_{1} P F_{1} ∢ = B P C ∢

, mert a

B P F_{1}

szög közös részük, nem közös

E_{1} P B

, illetőleg

F_{1} P C

részük pedig egyenlő a vele egy íven nyugvó

E_{1} Q B

, illetőleg

F_{1} Q C = F Q C

szöggel, ha

F_{1}

Q F

szakaszon, vagy annak

Q

végpontjában van, ‐ az utóbbi szögek viszont csúcsszögek. Ha pedig

F_{1}

Q E

szakaszon van, akkor az

E_{1} Q B

szög külső szöge az

F_{1} P C Q

húrnégyszögnek, az

F_{1} P C

rész-szög pedig belső szög a négyszög

Q

-val szemben fekvő csúcsánál, tehát a nem közös szög-részek egyenlősége ilyenkor is fennáll.

11. ábra

E_{1} F_{1}

szakasz része az

E F

szakasznak, az

E_{1} P F_{1}

szög része az

E P F

szögnek, tehát valóban fennáll

E P F ∢ > B P C ∢

. (Bizonyítani kellene még az

E_{1}

F_{1}

pontok helyzetéről felhasznált állítást.)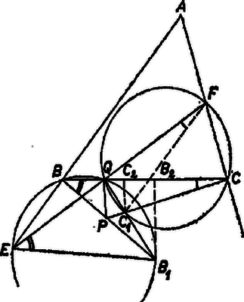

12. ábra

III. megoldás. Állítsunk merőlegest

Q

-ban

E F

-re, és messe ez a

P C

egyenest

C_{1}

-ben,

P B

-t pedig

B_{1}

-ben;

B_{1}

és

C_{1}

merőleges vetülete a

B C

egyenesen legyen

B_{2}

, ill.

C_{2}

(12. ábra).

E

A B

oldal meghosszabbításán van, ezért a merőleges a

P Q C

derékszögű szögtartományban halad, tehát a

B C P

háromszög

P C

oldalát és a

B P

oldal meghosszabbítását metszi, továbbá

C_{2}

Q C

szakaszon adódik. Ezért

Q C_{1} < Q B_{1}

, és egyszersmind

\begin{matrix} Q C_{2} < Q B_{2} . \end{matrix}

(15)

C

és

Q

rajta van a

C_{1} F

átmérő fölötti Thales-körön. A

Q F C_{1}

és

Q C C_{1}

szögek egyenlők, mint ugyanazon íven nyugvó kerületi szögek, így a

Q F C_{1}

és

C_{2} C C_{1}

derékszögű háromszögek hasonlók. A két átfogó közül

F C_{1}

a nagyobb, mert a körnek átmérője, tehát a megfelelő befogókra

\begin{matrix} F Q > C C_{2} . \end{matrix}

(16)

B C

-ből még fennmaradt

C_{2} B

szakasz helyett a nála nagyobb

B_{2} B

-ről mutatjuk meg, hogy kisebb az

E F

-ből fennmaradt

E Q

-nál. (

B_{2} B

B C

-nél nagyobb is lehet.) Ehhez a

B B_{1} B_{2}

és az

E B_{1} Q

háromszögeket hasonlítjuk össze.

B

és

Q

rajta van az

E B_{1}

átmérő fölé rajzolt Thales-körön, ezért egyrészt

\begin{matrix} E B_{1} > B B_{1}, \end{matrix}

másrészt a két háromszögben az egy íven nyugvó

B_{1} E Q

és

B_{1} B Q

kerületi hegyes szögek egyenlők. Így a két háromszög hasonló, és az

E B_{1} Q

háromszög oldalai nagyobbak, tehát

\begin{matrix} E Q > B B_{2} . \end{matrix}

(17)

Most már a (15)‐(17) egyenlőtlenségek alapján valóban

\begin{matrix} E F = E Q + Q F > B B_{2} + C_{2} C = B Q + Q B_{2} + C_{2} C > B Q + Q C_{2} + C_{2} C = B C . \end{matrix}

13. ábra

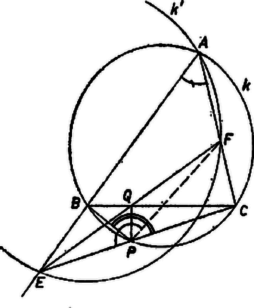IV. megoldás. A feladat állítása következik abból is, ha megmutatjuk, hogy az

A E F

háromszög köré írt

k'

kör átmérője nagyobb, mint az

A B C

háromszög köré írt

k

kör átmérője (13. ábra), hiszen nagyobb körben ugyanakkora kerületi szög ‐ ti. a

B A C = E A F

szög ‐ nagyobb húr felett nyugszik.
A

k

kör átmegy

P

-n is, és

A P

a kör egy átmérője, mert az

A B P C

négyszögben a

B

és

C

csúcsnál derékszög van. Elég tehát belátnunk, hogy

P

k'

kör belsejében van, hiszen ekkor

k'

-nek van

k

átmérőjénél nagyobb húrja, ezért

k'

átmérője nagyobb, mint

k

átmérője.

P

valóban

k

belsejében van, mert (8) alapján

\begin{matrix} E F P ∢ > B P C ∢ = 180^{\circ} - B A C ∢ = 180^{\circ} - E A F ∢, \end{matrix}

és az

E F

szakasz a

k'

kör (

A

-t nem tartalmazó)

E F

ívének pontjaiból látszik

180^{\circ} - E A F

szög alatt. Ennél nagyobb szög alatt az

E F

szakaszt csak a

k'

kör belső pontjaiból lehet látni. Ezt akartuk bizonyítani.

¹Ugyanis az

F F_{1}

szakasz

P

-n átmenő felező merőlegesének ugyanazon oldalára esik

E

és

F_{1}