Feladat: 1964. évi Matematika OKTV I. forduló 1. feladata Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1964/november, 97 - 99. oldal  PDF  |  MathML 
Témakör(ök): Négyszögek geometriája, Tengelyes tükrözés, Pont körüli forgatás, Transzformációk szorzata, Thalesz-kör, OKTV
Hivatkozás(ok):Feladatok: 1964/november: 1964. évi Matematika OKTV I. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Szorítkozzunk egyelőre arra az esetre, amikor B2 és C2 a BC egyenesnek ugyanazon az oldalán van, vagyis amikor a háromszög B-nél és C-nél levő szöge hegyesszög.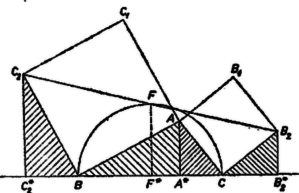
Vetítsük az A, B2, C2 pontokat és a C2B2 szakasz F felezőpontját a BC egyenesre, legyenek vetületeik rendre A*, B2*, C2* és F* (1. ábra). Minthogy a négyzeteket kifelé szerkesztettük, B2* ill. C2* a BC szakasz C-n, ill. B-n túli meghosszabbításán van.

 
 
1. ábra
 

A C2C2*B és BA*A derékszögű háromszögek egybevágók, mert C2B=BA, és C2*C2B∢=A*BA∢ merőleges szárú hegyesszögek. Hasonlóan az AA*C és CB2*B2 derékszögű háromszögek is egybevágók. Ezekből következik, hogy a C2C2*B2*B2 trapéz két párhuzamos oldalának összege
C2C2*+B2B2*=BA*+A*C=BC,
és így a trapéz középvonalának hossza
FF*=BC2,
továbbá ez a középvonal merőleges BC-re. Ez azt jelenti, hogy F a BC egyenes F* pontjától és egyszersmind magától az egyenestől is BC/2 távolságra van.
Bebizonyítjuk még, hogy F* a BC szakasz felezőpontja. Ezekből már következik, hogy F rajta van a BC fölé, mint átmérő fölé rajzolt körön, mégpedig a BC-re merőleges átmérő egyik végpontja F.
F* egyrészt felezi a C2*B2* szakaszt, másrészt az F*C szakasz ugyanannyival kisebb F*B2*-nál, mint BF* a C2*F*-nál, tudniillik ‐ a fenti egybevágóságok szerint ‐ AA*-gal. Így F* valóban felezi a BC szakaszt. Ezzel a bizonyítást ‐ a tett megszorító feltétel teljesülése esetére ‐ befejeztük.
Ha az ABC háromszögben a B-nél és C-nél levő szögek valamelyike, mondjuk a C-nél levő, derékszög, akkor egyszerűbb helyzettel állunk szemben, mert B2 a BC egyenesen adódik, és a C2C2*B2*B2 trapéz szerepét a C2C2*B2 derékszögű háromszög veszi át; a bizonyítás ennek megfelelő, kézenfekvő egyszerűsítésekkel ebben az esetben is alkalmazható.
Ha pedig, mondjuk C-nél, tompaszög van, akkor a B2C2 és B2*C2* szakaszok metszik egymást, a C2C2*B2B2* trapéz átlói lesznek (2. ábra), FF* az ezek felezőpontjait összekötő szakasz. Ez ‐ mint könnyen bebizonyítható ‐ minden konvex trapézban egyenlő a párhuzamos oldalak különbségének felével, az utóbbiról pedig a hegyesszögű esetben alkalmazott gondolatmenettel belátható, hogy egyenlő a BC szakasznak a felével. Ezek szerint az állítás minden háromszögre érvényes.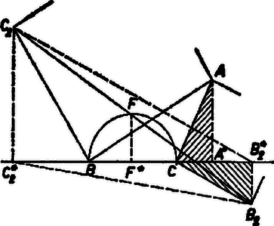
 
 
2. ábra
 

Megjegyzés. A fenti megoldáshoz hasonló gondolatmenettel ‐ alkalmas koordinátarendszert választva ‐ egyszerű analitikus geometriai megoldás is adható.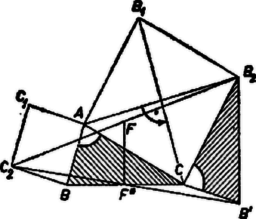
 
II. megoldás. Forgassuk el az ABC háromszöget az ACB2B1 négyzet középpontja körül 90∘-kal úgy, hogy A a C-be kerüljön. Így C a B2-be kerül, B elforgatott helyzete pedig legyen B' (3. ábra). Ekkor B'C merőleges BA-ra és egyenlő vele, tehát párhuzamos, egyenlő és egyező irányítású BC2-vel. Így B, C2, C, B' ebben a sorrendben paralelogrammát határoznak meg, tehát a BC átló F* felezőpontja a C2B' átlót is felezi.
 
 
3. ábra
 

A végzett forgatás folytán B'B2 merőleges BC-re és egyenlő vele. Most már az FF* szakasz a C2B2B' háromszög középvonala, tehát egyenlő a B'B2 és BC szakaszok felével. Ezek szerint B, C és F egyenlő távolságra vannak F*-tól, ez pedig azt jelenti, hogy F a BC átmérő fölé rajzolt körön van.
Ez a bizonyítás tetszés szerinti alakú ABC háromszög esetén érvényes.
 
III. megoldás. Forgassuk el az ABC háromszöget előbb B körül 90∘-kal úgy, hogy A a C2-be jusson, majd C körül 90∘-kal úgy, hogy A a B2-be jusson, legyen az első esetben C új helyzete C0, a második esetben B új helyzete B0 (4. ábra). A két forgatás ellentétes irányú, a négyzetek kifelé való szerkesztése miatt. A két forgatási szög összege 180∘, ezért BC2 és B0B2 párhuzamosak és ellentétes irányúak. Továbbá egyenlőek is, és ezért a BC2B0B2 négyszög paralelogramma. Így a C2B2 átló kérdéses F felezőpontja a BB0 átlót is felezi.
Másrészt a forgatásokból következik, hogy a BC0B0C négyszög négyzet, tehát az átlók közös F felezőpontjából az oldalak derékszögben látszanak, így F a BC oldal, mint átmérő fölé rajzolt Thales-körön van, éppen a BC-re merőleges átmérő egyik végpontja.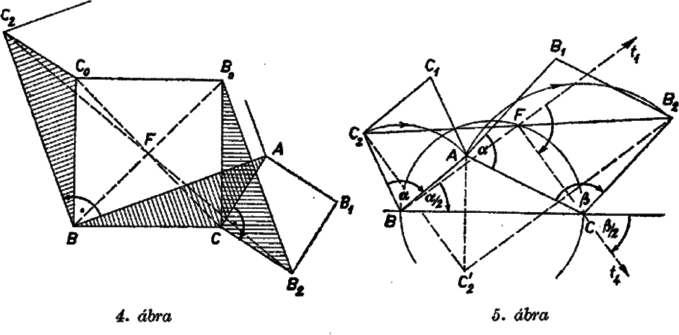
 
 
IV. megoldás. A C2 pontot átvihetjük B2-be úgy, hogy elforgatjuk először B körül α=90∘-kal, ‐ így A-ba kerül ‐, majd A-t elforgatjuk C körül ugyanabban az irányban β=90∘-kal (5. ábra).
Ismeretes, hogy egy (síkbeli) forgatás helyettesíthető bármely két olyan egymás utáni tükrözéssel, amelyek tengelye átmegy a forgatás középpontján, és az első tengelyt a második tengelybe átvivő forgatás fele akkora szögű, mint az eredeti forgatás, és azzal megegyező irányú.
Helyettesítsük a mondott forgatásokat két-két tükrözéssel úgy, hogy ezek t1, t2 és t3, t4 tengelypárja közül t2 és t3 azonos legyen. Így ugyanis a harmadik tükrözés visszaállítja a második tükrözés előtti helyzetet, és a négy tükrözés kettőre csökkenthető. Mivel t2 nek B-n, t3-nak C-n kell átmennie, így mindkettőnek egyaránt a BC egyenest kell választanunk. Ilyen választás mellett C2-t a B-n áthaladó és BC-vel α/2 szöget bezáró t1, majd a C-n átmenő és BC-vel β/2 szöget bezáró t4 tengelyen való tükrözés viszi át B2-be.
Ez a két tükrözés ‐ az idézett tétel megfordítása alapján ‐ helyettesíthető egyetlen forgatással, amelynek középpontja a t1 és t4 metszéspontja, szöge kétszer akkora, mint a t1-et t4-be átvivő forgatás, és iránya megegyezik az utóbbi forgatás irányával. A két tengely szöge (mint a t1, t2 és t4 határolta háromszög külső szöge)
α2+β2=90∘,(1)
így C2-t a B2-be 180∘-os forgatás viszi át, vagyis a tengelyek metszéspontja éppen a B2C2 szakasz F felezőpontja.
Mivel pedig az F pontból a BC szakasz 90∘-os szögben látszik, azért F rajta van a BC átmérőjű Thales-körön, ezt kellett bizonyítanunk.
 
Megjegyzés. A bizonyításban α-ról és β-ról csak azt használtuk fel (1)-ben, hogy összegük 180∘. A feladat állítása tehát helyes marad akkor is, ha a háromszög AB és AC oldalára kifelé olyan rombuszokat rajzolunk, melyeknek B-nél, ill. A-nál levő szöge egyenlő; továbbá akkor is, ha mindkét oldalra befelé rajzoljuk a rombuszokat. Az általánosított állítás bizonyítható ‐ értelemszerű módosításokkal a II. és III. megoldás gondolatmenetével is.