Kezdőlap


Feladat:	1963. évi Matematika OKTV I. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1963/november, 100 - 102. oldal		PDF \| MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Síkra vonatkozó tükrözés, Gúlák, Derékszögű háromszögek geometriája, OKTV
Hivatkozás(ok):	Feladatok: 1963/november: 1963. évi Matematika OKTV I. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a tégla csúcsait $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ , $H$ -val ( $A B C D$ egy határlap és $A E ‖ B F ‖ C G ‖ D H$ ); $a$ , $b$ , $c$ legyen rendre az $A B$ , $A D$ , $A E$ élek hossza. A testátlók hosszát jelöljük $d$ -vel, a tégla középpontját $O$ -val; tudjuk, hogy 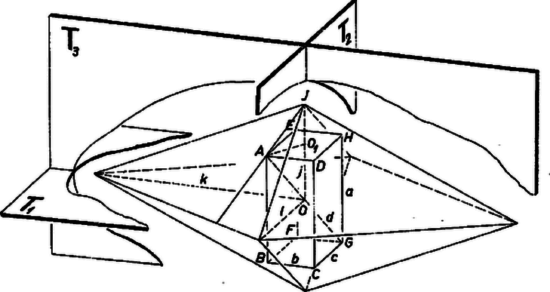$d^{2} = a^{2} + b^{2} + c^{2}$ .
Állapítsuk meg először az átlókra merőleges síkok közt keletkező $T$ test alakját. Az $A B$ , $A D$ , $A E$ élek $T_{1}$ , $T_{2}$ , $T_{3}$ felező merőleges síkjaira tükrözve a téglát, az önmagába megy át, testátlói ismét testátlókba, így az azokra merőleges síkok is egymásba mennek át, tehát a $T$ test is szimmetrikus $T_{1}$ , $T_{2}$ , $T_{3}$ -ra.
A szimmetriasíkok létesítette térnyolcadok mindegyike egy téglacsúcsot tartalmaz. Az ebben a megfelelő testátlóra merőlegesen állított sík a szimmetriasíkokkal egy-egy 3-oldalú gúlát határoz meg, melynek egyik csúcsa, $O$ , és az ebben találkozó lapjai, amelyek a szimmetriasíkokban vannak, páronként merőlegesek. A testátlóra merőleges sík valóban a szimmetriasíkok metszésvonalainak a térnyolcadot határoló félegyeneseit metszi, mert a testátló átmegy $O$ -n, ami a félegyenesek közös pontja és hegyes szöget alkot a félegyenesekkel. Egy ilyen gúla a szimmetriasíkokra való tükrözéssel sorra átvihető az összes többibe, és a 8 gúla együttesen alkotja $T$ -t, amelynek határfelülete így 8 egybevágó háromszögből áll, élei a szimmetriasíkokban vannak, csúcsai ezek metszésvonalain.

4. ábra

Könnyű belátni (ezt számításainkban nem fogjuk felhasználni), hogy az egy szimmetriasíkban levő élek egy-egy rombuszt alkotnak, ezen mint alapon nyugvó két egyenes gúlából tevődik össze

T

. Az ilyen testet a kristálytanban rombos bipiramisnak nevezik.

T

térfogata a szimmetriasíkok közti egy nyolcadba eső háromoldalú gúla térfogatának 8-szorosa, felszíne pedig a téglacsúcson átmenő határlap

t

területének 8-szorosa. Jelöljük a szóban forgó gúlának a tégla

A B

A D

A E

éleivel párhuzamos éleinek hosszát

j

k

l

-lel, akkor térfogatát kétféle úton is kiszámíthatjuk: mint a merőleges élek hossza szorzatának a hatodát, és mint

t

-nek és a rá merőleges téglaátló felének

1 / 3

-szoros szorzatát:

\begin{matrix} \frac{1}{6} j k l = \frac{1}{6} d \cdot t . \end{matrix}

Így

T

térfogatára,

V

-re, ill. felszínére,

F

-re

\begin{matrix} V = \frac{8}{6} j k l = \frac{4}{3} j k l és F = 8 t = 8 \frac{j k l}{d}, \end{matrix}

tehát a kettő között a következő összefüggés áll fenn:

\begin{matrix} F = \frac{6 V}{d} . \end{matrix}

Elég tehát

F

és

V

egyikét meghatározni.

V

-t lesz könnyebb, illetőleg a kiszámításához szükséges

j

k

l

szakaszokat.
Jelöljük az

A

-t tartalmazó térnegyedbe eső gúla

j

hosszúságú élének

O

-tól különböző végpontját

J

-vel, az él metszéspontját az

A D H E

lappal (e lap középpontját)

O_{1}

-gyel. Ekkor

O O_{1} = a / 2

, továbbá

J A

O A

-ra

A

-ban emelt merőleges sík egy egyenese, s így merőleges

O A

-ra. Az

A J O

és

O_{1} A O

derékszögű háromszögek hasonlók, mert

O

-nál levő hegyesszögük közös; így

\begin{matrix} \frac{j}{d / 2} = \frac{O J}{O A} = \frac{O A}{O O_{1}} = \frac{d / 2}{a / 2}, j = \frac{d^{2}}{2 a} = \frac{a^{2} + b^{2} + c^{2}}{2 a} . \end{matrix}

Ugyanígy látható, hogy

\begin{matrix} k = \frac{d^{2}}{2 b}, l = \frac{d^{2}}{2 c} . \end{matrix}

Így a keresett mennyiségek

\begin{matrix} V = \frac{4}{3} \cdot \frac{d^{6}}{8 a b c} = \frac{1}{6} \cdot \frac{{(a^{2} + b^{2} + c^{2})}^{3}}{a b c}, \\ F = \frac{6 V}{d} = \frac{d^{5}}{a b c} = \frac{{(\sqrt[]{a^{2} + b^{2} + c^{2}})}^{5}}{a b c} . \end{matrix}