Kezdőlap


Feladat:	1963. évi Matematika OKTV I. forduló 1. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1963/november, 97 - 98. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Háromszögek egybevágósága, Derékszögű háromszögek geometriája, Tengelyes tükrözés, Négyszögek középvonalai, Paralelogrammák, Téglalapok, Pitagorasz-tétel alkalmazásai, OKTV
Hivatkozás(ok):	Feladatok: 1963/november: 1963. évi Matematika OKTV I. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzés: Egyenlő szárú trapézon olyant szokás érteni, amely szimmetrikus a párhuzamos oldalakra merőleges tengelyre nézve, és az alábbiakban mi is ezt fogjuk érteni rajta. Az elnevezés jelentése szerint minden paralelogramma is trapéz egyenlő szárakkal (és egyenlő párhuzamos oldalakkal). Így ha $a = b$ , és a paralelogrammákat is tekintetbe vesszük, akkor egy $a$ hosszúságú $E F$ szakasz mint átmérő fölé rajzolt félkör bármely pontjából mint egyik csúcsból rajzolva olyan paralelogrammát, amelyiknek $E F$ középvonala, a feltételeknek megfelelő, ,,egyenlő szárú trapéz''-t kapunk, a terület tehát határozatlan. Így csak érdektelen eseteket zártunk ki. Az $a = b$ esetet is kizárhatjuk, mert ebben az esetben az elfogadott értelmezés mellett trapézunk téglalap, és így mindegyik oldal felezőpontjának vetülete a szemben levő oldalon annak a felezőpontja.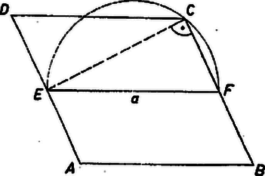

1. ábra

I. megoldás. Ha

a

-t és

b

-t ismerjük, akkor elég a magasság meghatározása a terület kiszámításához. Ehhez tájékozódunk először a trapéz alakjáról. Legyen a

D A

szár felezőpontja

E

, vetülete a

B C

száron a

C

csúcs. Ekkor

E

B C D

szögtartomány belsejében van, s így

\begin{matrix} D C B ∢ > E C B ∢ = 90^{\circ}, \end{matrix}

tehát

C

-nél és a szimmetria folytán

D

-nél is tompa szög van. Így, ha

a > b

, akkor

A B = a

C D = b

.
Tükrözzük a

C D E

háromszöget az

E

pontra. Ekkor a

D

pont

A

-ba kerül,

C

pedig a

C E

és

B A

szakaszok meghosszabbításainak

C'

metszéspontjába. Így a trapéz

t

területe egyenlő a

B C C'

derékszögű háromszögével. Jelöljük a

C

pont vetületét

A B

-n

M

-mel és

C M

-et

m

-mel, így

\begin{matrix} t = \frac{B C' \cdot m}{2}, \end{matrix}

és, felhasználva a derékszögű háromszög magasságának mértani közép tulajdonságát,

\begin{matrix} m^{2} = B M \cdot C' M, ahol B C' = a + b . \end{matrix}

B M

meghatározására tekintsük a

D

pont

N

vetületét is az

A B

oldalon. Egyrészt

M N = b

, másrészt a szimmetria miatt

A N = B M

és mivel a kettő együtt a párhuzamos oldalak különbségét adja, így

\begin{matrix} B M = \frac{a - b}{2}, C' M = a + b - \frac{a - b}{2} = \frac{a + 3 b}{2}, \\ m = \frac{\sqrt[]{(a - b) (a + 3 b)}}{2}, \end{matrix}

és a trapéz területe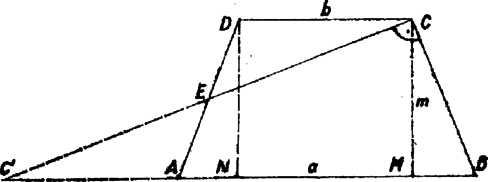

\begin{matrix} t = \frac{(a + b) \sqrt[]{(a - b) (a + 3 b)}}{4} . \end{matrix}

2. ábra

II. megoldás. Az

m

magasság meghatározására vegyük figyelembe, hogy a trapéz szimmetriája folytán a

B C

szár

F

felezőpontjának az

A D

száron a vetülete a

D

csúcs, a

C E F

és

D F E

derékszögű háromszögek egybevágók. Tükrözzük a

C E F

háromszöget

E F

-re. Mivel a középvonal

A B

-től és

C D

-től egyenlő távol fut, velük párhuzamosan, így

C

tükörképe az

A B

-n levő

M

vetülete. A

D E M F

négyszög szemben fekvő oldalai egyenlők, így a négyszög paralelogramma, éspedig téglalap, mert

D

-nél (és

M

-nél) levő szögéről tudjuk, hogy derékszög. Ennek folytán átlói egyenlők:

D M = E F = (a + b) / 2

, és a

C D M

derékszögű háromszögből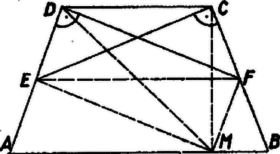

\begin{matrix} m^{2} = C M^{2} = D M^{2} - C D^{2} = {(\frac{a + b}{2})}^{2} - b^{2} = \frac{(a + 3 b) (a - b)}{4} . \end{matrix}

Megjegyzés: Több más út is választható

m

meghatározására, vagy kiszámíthatjuk a

B C

szár hosszát és annak ismeretében az I. megoldásban szereplő

B C C'

háromszög

C C'

befogóját, a területet pedig a

t = B C \cdot C C' / 2

összefüggésből. A fenti két számítás látszik még legegyszerűbbnek.

3. ábra