Feladat: 1962. évi Matematika OKTV II. forduló 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Füzet: 1962/december, 197 - 205. oldal  PDF  |  MathML 
Témakör(ök): Hozzáírt körök, Szögfelező egyenes, Háromszögek hasonlósága, Tengelyes tükrözés, Középponti és kerületi szögek, Egyenesek egyenlete, Kör egyenlete, Beírt kör, OKTV
Hivatkozás(ok):Feladatok: 1962/szeptember: 1962. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Azt fogjuk megmutatni, hogy az M pont minden helyzeténél a PC egyenes párhuzamos OA-val, ehhez azonban előbb megvizsgáljuk a P pont lehetséges helyzeteit a körhöz és t-hez viszonyítva.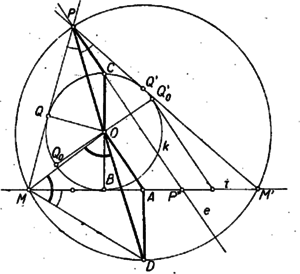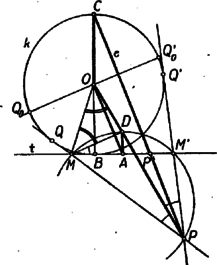
Van az M, M' pontpárnak egy olyan helyzete, amelyben a k-hoz húzott második érintők párhuzamosak. Ezt a pontpárt úgy kaphatjuk meg, hogy k-nak az AO-ra merőleges átmérője végpontjaiban, (Q0, Q0'-ben) húzunk érintőket. Ezek A-ra szimmetrikus pontpárt metszenek ki t-ből, mert OA a köztük levő sáv középvonala. Ha M, M' a sávon kívül van, akkor Q, Q' a C-t tartalmazó Q0, Q0' félkörön van, így a második érintők metszik egymást, még pedig t-nek azon a partján, amelyiken k van; így k a PMM' háromszögnek beírt köre (4. ábra).

 
 
4. ábra
 
 
5. ábra
 

Ha M, M' a két párhuzamos közt van, akkor Q, Q' a B-t tartalmazó Q0, Q0' félkörön van, így most is metszik egymást az érintők. Ha az M, M' pontpár közrefogja B-t, akkor Q és Q' is közrefogja B-t a félkörön. Ekkor P a t érintő ellenkező partján keletkezik, mint k, és k a PMM' háromszög MM' oldalához hozzáírt kör (5. ábra).
Ha M és M' egyike B-be esik, és ez különbözik A-tól, akkor ebből a pontból nem húzható t-től különböző érintő, viszont tekinthetjük a második érintőnek is t-t. A másik pont ekkor B-nek A-ra vonatkozó tükörképe, és ez a két második érintő metszéspontja is, tehát a mértani helynek az M és M' mondott helyzetéhez tartozó pontja is.
Ha végül az M és M' pontok egyike A és B közé esik, akkor P a másik pontból húzott érintőnek az érintkezési pont és a t egyenes közé eső szakaszán keletkezik. Ekkor k a PMM' háromszög egyik olyan hozzáírt köre, amelyik az MM' oldal meghosszabbítását érinti (6. ábra).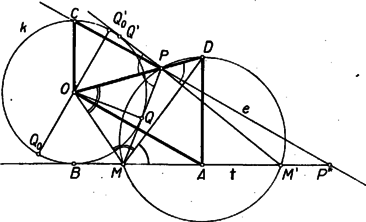
 
 
6. ábra
 

Ha A egybeesik B-vel, akkor k is, t is, az M, M' pontpár is, így a belőlük húzott érintőpár is tükrös a BC egyenesre, tehát a P pont ezen az egyenesen van. Az egyenes bármely a körön kívüli pontjából két szimmetrikus érintő húzható k-hoz, ezek szimmetrikus M, M' pontpárt metszenek ki t-ből, amiből kiindulva éppen a kiszemelt P pontot kapjuk meg. A B és C pontban csak egy-egy érintő húzható k-hoz; az utóbbi nem metszi t-t, az előbbi viszont éppen t, így nem adható meg olyan pontpár, amelyikből kiindulva B-t vagy C-t kapnánk a mértani hely pontjaiként. Ebben az esetben tehát a BC egyenes k-n kívüli két félegyenese a keresett mértani hely. (A PC és OA egyenes ebben az esetben egybeesik, ami megfelel állításunknak.)
Tegyük fel a továbbiakban, hogy A és B különböző.
Nyilvánvaló, hogy M és M' felcserélésével ismét A-ra tükrös pontpárt kapunk, a hozzájuk tartozó P pont pedig nem változik. Így elegendő azokat a P pontokat vizsgálni, amelyek az A-ból B-n át húzott félegyenesen levő M pontokhoz tartoznak; hiszen ha M a másik félegyenesen fut végig, akkor P az előbbi M pontokhoz tartozó mértani helyet futja be mégegyszer.
Térjünk most állításunk bizonyítására. Az O pont a PMM' háromszög P-ből induló belső vagy külső szögfelezőjén van, aszerint hogy k az MM' szakaszt érinti, vagy annak meghosszabbítását. Jelöljük a kérdéses szögfelező és a PMM' háromszög köré írt kör metszéspontját D-vel. A belső szögfelező metszéspontja a P-t nem tartalmazó MM' ív felezőpontja, mivel pedig a belső és külső szögfelező egymásra merőleges, így P és a két szögfelező k-val való metszéspontja derékszögű háromszöget alkot. Ennek átfogója a körnek átmérője. Így a külső szögfelező a körülírt kört a belső szögfelező metszéspontjával árellenes pontban, vagyis a P-t tartalmazó MM' ív felezőpontjában metszi. Bármelyik pontból bocsátunk is merőlegest MM'-re, az azt felezőpontjában, A-ban metszi.
Állításunkat úgy bizonyítjuk, hogy megmutatjuk mindegyik esetben a COP és ADO háromszögek hasonlóságát. Könnyű látni, hogy az OPQ és DMA derékszögű háromszögek hasonlók. Valóban, ha O a P-nél levő belső szög felezőjén van, akkor a kerületi szögek összefüggését felhasználva
DMA∢=DMM'∢=DPM'∢=DPM∢=OPQ∢.
Ha pedig O a külső szögfelezőn van, akkor
DMA∢=DMM'∢=DPM'∢=OPQ'∢=OPQ∢.
Az OPQ és DMA háromszög szögei tehát mindkét esetben megegyeznek s így
POOQ=MDDA.(1)

Itt OQ, mint körsugár, egyenlő OC-vel, állításunk igazolásához így szükségünk van annak a megmutatására, hogy DO=DM.
Ha k a PMM' háromszög beírt köre, akkor MO is a háromszög belső szögfelezője, s így, mint az MOP háromszög külső szöge
MOD∢=OPM∢+OMP∢=DMM'∢+OMM'∢=DMO∢.

Ha k az MM' oldalhoz hozzáírt kör, akkor MO a PMM' háromszög külső szögét felezi, s így ismét az MOP háromszögből indulva ki
MOD∢=180∘-(OPM∢+OMP∢)=180∘-(OPM∢+M'MP∢++OMM'∢)=180∘-(DMM'∢+M'MP∢+OMQ∢)=DMO∢.

Ha k a PMM' háromszög PM oldalához hozzáírt kör, akkor PO is, MO is a háromszög megfelelő külső szögét felezi, s így ismét az MOP háromszögből indulva ki
MOD∢=180∘-(OPM∢+OMP∢)=180∘-(DMM'∢+OMB∢)==DMO∢.

Eszerint az ODM háromszög OD-vel és DM-mel szemben levő szögei mindhárom esetben egyenlők, s így valóban OD=DM. Ezt, továbbá az említett OQ=OC egyenlőséget felhasználva (1)-ből
POOC=ODDA.

Az ADO és COP háromszögek itt szereplő oldalai párhuzamosak. Az első esetben D a t egyenes ellenkező partján van, mint k, s így DA és OB ellenkező irányban, DA és OC pedig egy irányban párhuzamos, DO és OP szintén.
A második és harmadik esetben D és k a t egyenes egy partján van, így DA és OC ellenkező irányban párhuzamos. Másrészt D a második esetben az OP szakaszon van, a harmadik esetben a szakasz P-n túli meghosszabbításán, így OD és PO is ellenkező irányban párhuzamosak. Ennek folytán az ADO és COP háromszög mindhárom esetben hasonló, mert két oldaluk aránya és a köztük levő szög megegyezik, és hasonló helyzetű is. Így a harmadik oldalpár is párhuzamos:
PC∥OA.

Eszerint P mindig a C ponton át az (M ponttól független) OA egyenessel párhuzamos e egyenesen van. Nyilván nem lehet az egyenes k körbe eső húrján.
 
Ha P az e egyenes egy a körön kívüli és nem a t-n levő pontja, akkor húzzuk meg belőle az egyik érintőt k-hoz és tükrözzük ennek t-vel való metszéspontját A-ra. Az így kapott pontpárt választva M, M'-nek, az ezekből húzott érintők metszik egymást, mert csak az OA-val (s így e-vel is) párhuzamos érintőpár nem metszi egymást. A metszéspont egyrészt a bizonyítottak szerint e-n van, másrészt a meghúzott érintőn, tehát a kiválasztott P pont.
Legyen e metszéspontja t-vel P* (7. ábra), ekkor OA párhuzamos a BCP* háromszög CP* oldalával és a BC oldal O felezőpontjából indul ki, tehát a háromszög középvonala; így A felezi a BP* szakaszt, vagyis P* a B pont tükörképe A-ra, de ekkor, mint a megoldás elején láttuk, a mértani hely B, P* pontpárhoz tartozó pontja 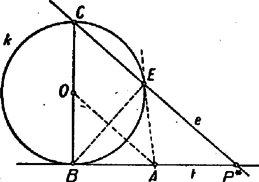P*.
 
 
7. ábra
 

Vizsgáljuk meg végül e metszéspontjait k-val. A C-ben húzott érintő párhuzamos t-vel, nem keletkezhet tehát annak semelyik pontjából húzott érintőként, és nem megy át rajta a kör más pontjához húzott érintő sem. Így C nem tartozik a mértani helyhez.
A másik E metszéspont nem más, mint az A-ból k-hoz húzott második érintő érintési pontja, ugyanis AO-ra tükrözve B-t a tükörkép egyrészt k-n van, mert annak középpontján átmenő egyenesre tükröztünk, másrészt e-n, mert egy háromszög egy csúcsát a szemközti oldallal párhuzamos középvonalra tükrözve a tükörkép a szemközti oldalán van. Így B tükörképe csak E lehet, és AE az AB egyenes tükörképe, tehát érinti a k kört.
Eszerint az E-ben húzott érintő A-ban metszi t-t. Ez a pont saját tükörképe, egybeeső M, M' pontpárt kapunk, a belőlük húzott második érintők is egybeesnek, tehát nincs meghatározott metszéspontjuk, s így E nem tartozik a mértani helyhez.
A keresett mértani hely tehát a C-n át AO-val párhuzamosan húzott (vagy C-n és az A-ból húzott érintő E érintési pontján át, vagy C-n és a B pont A-ra vonatkozó P* tükörképén át húzott) egyenesnek a k-n kívül eső két félegyeneséből áll.
 
II. megoldás. A P pont lehetséges helyzeteire vonatkozó megállapításokat nem ismételjük meg és csak azt az esetet vizsgáljuk, ha A≠B. Legyen D a B pont tükörképe A-ra. Azt fogjuk megmutatni, hogy P mindig a CD egyenesen van, mégpedig úgy, hogy először belátjuk, hogy ha k a PMM' háromszög beírt köre, akkor D az MM' oldalhoz hozzáírt kör érintési pontja, ha k az MM' oldalhoz hozzáírt kör, akkor D a beírt kör érintési pontja, ha pedig k az MP oldalhoz hozzáírt kör, akkor D az M'P oldalhoz hozzáirt kör érintési pontja. Jelöljük a második kört mindhárom esetben k*-gal, középpontját O*-gal.
Az első két esetben a P-ből induló oldalak k és k* közös külső érintői, MM' pedig az egyik közös belső érintő, a harmadik esetben pedig a P-n átmenő érintők a közös belső érintők, MM' pedig az egyik külső közös érintő. Állításunk ennek folytán úgy fogalmazható, hogy két kör egy közös külső érintőjén az érintési pontok közti szakasz, és a belső érintők metszéspontjai közti szakasz felezőpontja közös, és hasonlóan egy belső közös érintőn az érintési pontok és a külső közös érintők metszéspontja közti szakasz középpontja szintén azonos. Ezt fogjuk először bizonyítani.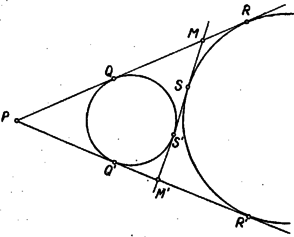
 
 
8. ábra
 

Legyen tehát két kör két közös külső érintőjének metszéspontja P, az egyik érintő érintse a köröket Q, ill. R pontban, a másik Q', ill. R'-ben (8. ábra). Egy közös belső érintő messe az előbbit egy M pontban, az utóbbit M'-ben, és legyen az M-hez közelebbi érintési pont S, a másik S'. Ekkor az egy pontból egy körhöz húzható érintők egyenlősége folytán
PR=PQ+QM+MR=PQ+S'M+SM=PQ+MM'+SM-M'S',
és hasonlóan

PR'=PQ'+Q'M'+M'R'=PQ'+M'S'+M'S=
   =PQ'+MM'-MS+M'S'.

Mivel még PR=PR' és PQ=PQ', így kell, hogy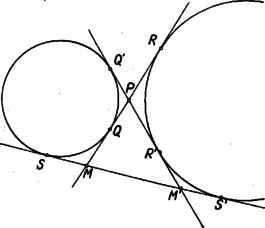
MS-M'S'=M'S'-MS,
amiből MS=M'S'. Ez pedig éppen azt jelenti, hogy az MM' és SS'szakaszok felezőpontja egybeesik.
 
 
9. ábra
 

Hasonló jelöléseket használva két közös belső érintő esetén (9. ábra)
PR=MR-PQ-QM=MS'-PQ-MS=MM'-PQ+M'S'-MS,
és hasonlóan
PR'=Q'M'-PQ'-R'M'=SM'-PQ'-M'S'=MM'-PQ'+SM-M'S'.
A két összefüggésből, mivel PR=PR', PQ=PQ', így ismét következik, hogy MS=M'S', s így az MM' és SS' szakaszok felezőpontja ez esetben is egybeesik.
Ez feladatunkra alkalmazva valóban azt adja, hogy mind a három esetben k és k* körök B és D érintési pontjai egymás tükörképei az MM' szakasz A felezőpontjára nézve, és ezt akartuk belátni.
P az első két esetben k és k* külső hasonlósági pontja, a harmadik esetben pedig belső hasonlósági pontjuk, így következik, hogy P, C és D egy egyenesen vannak, ha belátjuk, hogy a mondott P középpontú hasonlóságoknál a C és D pont mindig megfelelő pontok.
Az első és második esetben k és k* t különböző oldalán van (10. ábra), így OB, O*D ellenkező irányban merőlegesek t-re, OC és O*D tehát egyirányú párhuzamos sugarak, így a külső hasonlósági pontra nézve C és D a két kör egymásnak megfelelő pontjai.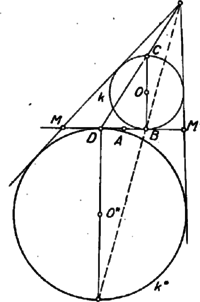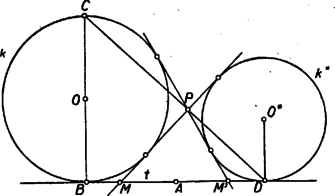
 
 
10. ábra
 
 
11. ábra
 

A harmadik esetben k és k* t-nek ugyanazon az oldalán van (11. ábra), így OB és O*D egy irányban, OC és O*D tehát ellenkező irányban párhuzamosak. P most belső hasonlósági pont, erre nézve C és D ismét egymásnak megfelelő pontok. Ezzel bebizonyítottuk, hogy C, D és P mindig egy egyenesen van, vagyis, mivel a C és D pontok nem változnak M-mel, a mértani hely pontjai a CD egyenesen vannak.
Az, hogy ennek az egyenesnek mely pontjai tartoznak a mértani helyhez, az előbbi megoldáshoz teljesen hasonlóan tárgyalható. Ezt itt nem ismételjük meg.
A versenyzők legtöbbje a koordinátageometria módszereivel kereste a mértani helyet. Bemutatunk egy ilyen megoldást.
 

III. megoldás. Válasszuk origónak a k kör O középpontját, távolságegységének a sugarát, és az X-tengely legyen párhuzamos t-vel úgy, hogy t a (0,-1) pontban érintse k-t. Jelöljük A abszcisszáját a-val, tehát A az (a,-1) pont (12. ábra). Az M és M' pontok a t-n vannak, tehát (z,-1), ill. (z',-1) alakúak a koordinátáik. Mivel a köztük levő szakasz felezőpontja A, így
z+z'=2a.(1)

 
12. ábra
 

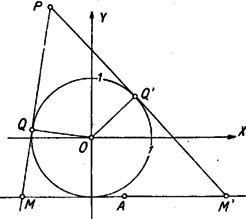Az M, ill. M' pontból húzott érintő érintse a kört a Q (u,v), ill. Q'(u',v') pontban. Ekkor
u2+v2=u'2+v'2=1,(2)
mert a pontok a körön vannak. Az OQ sugár iránytangense v/u (ha u≠0), így a Q-n át OQ-ra merőlegesen haladó egyenes egyenlete (ha v≠0)
y-v=-uv(x-u),vagyux+vy=u2+v2=1.
Az egyenlet megadja a Q-n átmenő érintőt az u=0 (v=1, vagy v=-1) és a v=0 (u=1, vagy u=-1) esetben is.
Ez az érintő átmegy M-en, tehát
uz-v=1,v=uz-1,
és ezt (2)-be írva
u2+(uz-1)2=1,u[(1+z2)u-2z]=0.
Hagyjuk egyelőre figyelmen kívül az u=0 esetet, ekkor
u=2z1+z2,ígyv=uz-1=z2-1z2+1,
és az M pontból húzott érintő egyenlete így írható:
2zx+(z2-1)y=z2+1.(3)
Hasonlóan az M' ponton átmenő érintő egyenlete:
2z'x+(z'2-1)y=z'2+1.(3a)

A P metszéspont xP, yP koordinátáit kiszámíthatjuk pl. úgy, hogy az első egyenlet z'-szöröséből levonjuk a második z-szeresét:
[z'(z2-1)-z(z'2-1)]yP=z'(z2+1)-z(z'2+1),(z-z')[(zz'+1)yP-zz'+1]=0.



Ismét hagyjuk figyelmen kívül egyelőre a z=z' esetet (amikor M és M' egybeesik, s így megegyezik A-val), ekkor, amennyiben zz'≠-1,
yP=zz'-1zz'+1,(4)
és ha z≠0, akkor pl. az M-ből húzott érintő egyenletéből
xP=z2+12z-z2-12z⋅zz'-1zz'+1=z+z'zz'+1=2azz'+1.(5)
(Felhasználtuk az (1) összefüggést.) Az utóbbi egyenletből, ha xP≠0
zz'=2axP-1,(6)
és ezt yP kifejezésbe beírva
yP=2axP-22axP=1-xPa,vagyxP+ayP=a.

A keresett mértani hely pontjai tehát az
x+ay=a(7)
egyenesen vannak, eltekintve esetleg a figyelmen kívül hagyott esetekhez tartozó pontoktól.
Vizsgáljuk meg, hogy (7) mely pontjai keletkeznek mint alkalmas M és M' pontokból húzott érintők metszéspontjai. Ezek azok a pontok, amelyek koordinátái alkalmas z és z' (valós) számokkal (4), (5) alakban írhatók. Az ilyen z (és (1) szerint neki megfelelő z') értéket az M-ből húzott érintő (3) egyenletéből számíthatjuk ki. Azt z szerint rendezve
(y-1)z2+2xz-y-1=0.
Innen
z=-x±x2+y2-1y-1,
tehát azokhoz az x, y értékpárokhoz, az egyenesnek azokhoz a pontjaihoz tartozik ilyen z érték, amelyekre
x2+y2-1≥0,
vagyis amelyek nincsenek a k körben, és amelyekre y≠1, tehát a körrel való (0,1) metszéspontot is figyelmen kívül kell hagynunk. A második metszéspontra x2+y2-1=0, de y≠1, így, felhasználva (7)-et
z=-xy-1=a,
ekkor (1)-ből z'=a. Az M és M' pont tehát egybeesik (és azonos A-val), így nincs a belőlük húzott érintőknek meghatározott metszéspontja. Ez a pont sem tartozik tehát a mértani helyhez. Ezzel a korábban kizárt z=z' esetet is elintéztük, mert (1) szerint ekkor közös értékük csak a lehet.
Meg kell még vizsgálnunk a korábban a tárgyalásból kizárt eseteket, hogy tartozik-e azokhoz és milyen pontja a mértani helynek. Természetesen minden kizárt esettel együtt az M helyett M'-re vonatkozó megfelelő esetet is tárgyalni kell, ez azonban a két pont szimmetrikus szerepe miatt nem fog külön feladatot jelenteni.
Korábban figyelmen kívül hagytuk az x=0 értéket. A (7) egyenes ehhez tartozó pontjának ordinátája y=1, és éppen láttuk, hogy ez sem tartozik a mértani helyhez.
Kizártuk azt, hogy az M (vagy M') pontból húzott érintő érintési pontjának u (vagy u') abszcisszája 0 legyen. Ebben az esetben az érintési pont csak (0,1) vagy (0,-1) lehet. Az előbbi eshetőséget már éppen kizártuk.
Az M-ből és M'-ből húzott ,,második'', azaz t-től különböző érintő viszont a (0,-1)-től különböző pontban érinti k-t, kivéve, ha M (ill. M') éppen a (0,-1) pont. Ekkor tekinthetjük ,,második'' érintőnek is a t egyenest. Mivel ekkor z (vagy z') 0, (1) miatta másik pont a (2a,-1) pont, és a két érintő metszéspontja is ez a pont, ami a (7) egyenes metszéspontja t-vel. Ezt tehát a mértani helyhez tartozónak tekinthetjük. Ezzel egyszersmind a z=0 és z'=0 esetet is megtárgyaltuk.
Kizártuk végül korábban a zz'=-1 esetet. Ekkor pl. az M-ből húzott érintő (3) egyenletét 0-ra redukálva és z'2-tel szorozva
2zz'2x+[(zz')2-z'2]y-(zz')2-z'2=-2z'z-(z'2-1)y-1-z'2=0.
Ez párhuzamos a másik érintővel, melynek (3a) egyenlete
2z'x+(z'2-1)y-1-z'2=0
alakban írható, de különbözik attól, tehát az ilyen z, z' értékpárhoz nem tartozik metszéspont.
Ezzel bebizonyítottuk, hogy a keresett mértani hely az x+ay-a=0 egyenesnek a körön kívül eső két félegyenese, ami nem más, mint az A-ból húzott érintő érintési pontját és a t érintési pontjával átellenes pontot összekötő húrnak a körön kívüli meghosszabbítása mindkét irányban.
 
Megjegyzések. 1. A zz'=-1 esetben (1)-ből z(2a-z)=-1, azaz z2=2az+1, és így az M-ből húzott érintő egyenlete ilyen alakban írható:
2zx+2azy=2az+2,x+ay=a+1z.
Ez párhuzamos a mértani hellyel. A föntiek szerint ugyanez áll az M'-ből húzott érintőre is.
2. A két érintő egyenletéből még egyszerűbben jutunk a mértani hely egyenletéhez, ha a két érintő 0-ra redukált egyenletének különbségét képezzük és felhasználjuk (1)-et:
0=2zx+(z2-1)y-1-z2-[2z'x+(z'2-1)y-1-z'2]==2(z-z')x+(z2-z'2)y-(z2-z'2)==(z-z')(2x+(z+z')y-(z+z')]=2(z-z')(x+ay-a).
Ha az (x,y) pont rajta van mind a két érintőn, akkor kielégíti az utolsó egyenletet és ha z≠z', akkor (7)-et is. Azt a z értéket, amely egy adott (x,y) ponthoz vezet, most is ugyanúgy kereshetjük meg, mint az előbb.
3. Sok versenyző nem kereste a számítások lehetőleg egyszerű útját, és így nem maradt kellő ideje terve teljes végrehajtására.