Kezdőlap


Feladat:	1962. évi Matematika OKTV II. forduló 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1962/december, 193 - 194. oldal		PDF \| MathML
Témakör(ök):	Térelemek és részeik, Szögfüggvények, síkgeometriai számítások, Pitagorasz-tétel alkalmazásai, Koszinusztétel alkalmazása, OKTV
Hivatkozás(ok):	Feladatok: 1962/szeptember: 1962. évi Matematika OKTV II. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $a$ félegyenes egy $S$ -től különböző pontja $A$ . Emeljünk $a$ -ra az $A$ pontban merőlegest $a$ és $c$ síkjában. Mivel $α$ hegyesszög, ez metszi a $c$ félegyenest egy $C$ pontban. Hasonlóan $c$ -re $C$ pontjában merőlegest állítva $c$ és $b$ síkjában, ez metszi $b$ -t egy $B$ pontban (1. ábra).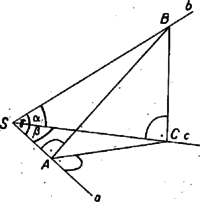

1. ábra

A

B

C

-n átmenő

Σ

sík merőleges

a

-ra, ugyanis

A C

egyenese szerkesztés szerint merőleges

a

-ra, a

C B

egyenes pedig az

S A C

síkra merőleges

S C B

síkban van és merőleges a két sík

S C

metszésvonalára, így

C B

merőleges az

S A C

síkra, tehát annak minden egyenesére, így

a

-ra is.

A C

és

C B

tehát a

Σ

sík két

a

-ra merőleges egyenese, amelyek nem párhuzamosak. Így

Σ

merőleges

a

-ra, és az

S A C

szög mellett, ami szerkesztés szerint derékszög, derékszög az

S A B

szög is, és az

A C B

szög is, mert

A C

szára az

S A C

síkban van,

C B

pedig merőleges erre a síkra. Az

S C B

szög a szerkesztés szerint ugyancsak derékszög. A feladat feltételei szerint

B S C ∢ = α

C S A ∢ = β

, és az

A S B ∢ = γ

szöget kell kiszámítanunk.
Most már az

S B C

, illetőleg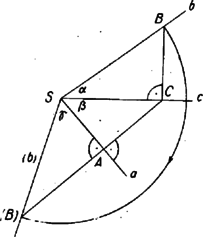

S C A

háromszögből

S C = S B cos α

S A = S C cos β

, és így az

S B A

háromszögből

\begin{matrix} cos γ = cos A S B ∢ = \frac{S A}{S B} = \frac{S C}{S B} cos β = cos α cos β . \end{matrix}

2. ábra

Megjegyzés. A felhasznált összefüggéseket még világosabbá tehetjük ábrázoló geometriai meggondolással. Tekintsük az

a

c

síkot első képsíknak, a

b

c

síkot második képsíknak, ekkor

c

a képsíkrendszer tengelyében van. A képsíkoknak az

a

, ill.

b

félegyenest tartalmazó félsíkjait, vegyük pozitívnak. Az

a

és

b

félegyenesekkel meghatározott síkot

a

‐ mint a sík első nyomegyenese ‐ körül az első képsíkba leforgatva a 2. ábrát kapjuk, ezen mindhárom felhasznált derékszögű háromszög valódi nagyságban látható.

(B)

-et ‐ különbségi háromszög mellőzésével ‐ kimetszhetjük a

C

-n át

a

-ra állított merőlegesből az

S B = S (B)

egyenlőség alapján, ugyanis az

S B

szakasz mind a második képsíkon, mind a leforgatásban valódi nagyságban látszik.
A legtöbb versenyző több trigonometriai ismeret felhasználásával ‐ de viszont kevesebb diszkusszióval ‐ végezte el a számítást. Ilyen a következő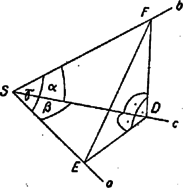

3. ábra

II. megoldás. Legyen a

c

félegyenes egy

S

-től különböző pontja

D

, és emeljünk

c

-re merőlegest mind az

a

c

, mind a

b

c

síkban. Mivel

α

és

β

hegyesszögek, ezek metszik

a

-t

E

-ben, ill.

b

-t

F

-ben (3. ábra). Az

E D F

szög az

S D E

és

S D F

síkok hajlásszöge, tehát a

D E F

háromszögben

D

-nél derékszög van, továbbá az

S E D

és

S F D

háromszögek is derékszögűek. A keresett

γ

szöget tartalmazó

S E F

háromszög mindhárom oldalát kifejezhetjük

S D

-vel és az ismert szögekkel:

\begin{matrix} S E = \frac{S D}{cos α}, S F = \frac{S D}{cos β}, \end{matrix}

továbbá

D E = S D tg β

D F = S D tg α

,

és így

\begin{matrix} E F = \sqrt[]{D E^{2} + D F^{2}} = S D \sqrt[]{{tg}^{2} α + {tg}^{2} β} . \end{matrix}

Ezekkel a koszinusz-tétel alapján

\begin{matrix} cos γ = cos E S F ∢ = \frac{S E^{2} + S F^{2} - E F^{2}}{2 S E \cdot S F} . \end{matrix}

A számláló jól ismert azonosságok felhasználásával így alakítható:

\begin{matrix} S E^{2} & + S F^{2} - E F^{2} = S D^{2} (\frac{1}{cos^{2} α} + \frac{1}{cos^{2} β} - {tg}^{2} α - {tg}^{2} β) = \\ = S D^{2} (\frac{sin^{2} α + cos^{2} α}{cos^{2} α} - {tg}^{2} α + \frac{sin^{2} β + cos^{2} β}{cos^{2} β} - {tg}^{2} β) = 2 S D^{2}, \end{matrix}

tehát

\begin{matrix} cos γ = 2 S D^{2} : \frac{2 S D^{2}}{cos α cos β} = cos α cos β . \end{matrix}

Megjegyzés. Több versenyző rámutatott, hogy hasonlóan számíthatjuk

γ

-t akkor is, ha az

a

c

és

b

c

félegyenes-párokkal meghatározott síkok szöge tetszés szerinti

ε

szög. Az

E D F

szög éppen ezt a lapszöget méri, tehát

\begin{matrix} E F^{2} = D E^{2} + D F^{2} - 2 D E \cdot D F cos ε, \end{matrix}

és így

D E / S E = sin β

D F / S F = sin α

figyelembevételével

\begin{matrix} cos γ = cos α cos β + sin α sin β cos ε . \end{matrix}

Ezt az összefüggést a gömbháromszögtan oldal-koszinusz-tételének szokás nevezni; érvényességének feltételeivel itt tovább nem foglalkozunk.