Feladat:	1961. évi Matematika OKTV II. forduló 3. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1962/január, 3 - 4. oldal		PDF  |  MathML
Témakör(ök):	Pitagorasz-tétel alkalmazásai, Teljes indukció módszere, OKTV
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Matematika OKTV II. forduló 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.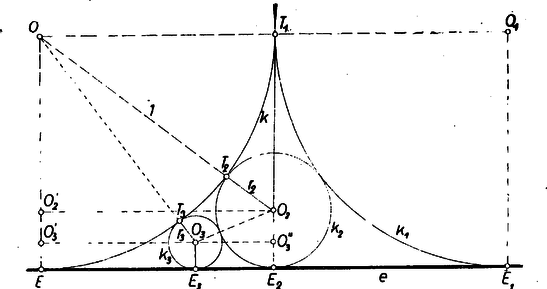     Legyen $k$ és $k_1$ középpontja $O$, $O_1$, $e$-vel való, valamint közös érintkezési pontjuk $E$, $E_1$, ill. $T_1$. Nyilvánvaló, hogy $k_2$ az $E{E}_1$ szakasszal és az $E{T}_1$, $E_1{T}_1$ negyedkörívekkel határolt síkrészben helyezkedik el, $k$-t és $k_1$-et kívülről érinti, és $O_2$ középpontja az $E_{1}E$ szakasz felező merőlegesén van. $k_2$ sugarát $r_2$-vel, $k$-n, ill. $e$-n való érintési pontját $T_2$, ill. $E_2$-vel, és $O_2$-nek $OE$-n való vetületét $O{\text{'}}_2$-vel jelölve az $O{O}_{2}O{\text{'}}_2$ derékszögű háromszögből $\begin{array}{c}{\displaystyle O{O}_2^2=O_{2}O{\text{'}}_2^2+OO{\text{'}}_2^2=E_2{E}^2+{\left(OE-O{\text{'}}_{2}E\right)}^2\mathrm{,}}\end{array}$ azaz $\begin{array}{c}{\displaystyle {\left(1+r_2\right)}^2=1+{\left(1-r_2\right)}^2\mathrm{,}}\end{array}$ és így $r_2=1/4$. Világos, hogy $k_3$ gyanánt nem $k_1$-et, hanem az $E{E}_2$ szakasszal és az $E{T}_2$, $E_2{T}_2$ ívekkel határolt síkrészben fekvő kört kell tekintenünk, és hogy a $k_4\mathrm{,}{k}_5\mathrm{,}\text{...}\mathrm{,}{k}_n$ körök is minden kisebb sorszámú körtől különbözők. Legyen a körsorozat két egymás utáni tagja $k_i$ és $k_{i+1}$, sugaruk $r_i$, $r_{i+1}$, érintkezési pontjuk $k$-val, ill. $e$-vel $T_i$, $T_{i+1}$, $E_i$, $E_{i+1}$, középpontjuk $O_i$, $O_{i+1}$, és ennek vetülete $OE$-re $O{\text{'}}_i$, ill. $O{\text{'}}_{i+1}$, végül $O_{i+1}$ vetülete $O_i{E}_i$-re $O\text{'}{\text{'}}_{i+1}$ (az ábrán az $i=2$ eset látható). Ekkor az $O{O}_{i}O{\text{'}}_i$, $O{O}_{i+1}O{\text{'}}_{i+1}$, $O_i{O}_{i+1}O\text{'}{\text{'}}_{i+1}$ derékszögű háromszögből: $\begin{array}{c}{\displaystyle E{E}_i=O{\text{'}}_i{O}_i=\sqrt[]{O{O}_i^2-{\left(OE-O{\text{'}}_{i}E\right)}^2}=\sqrt[]{{\left(1+r_i\right)}^2-{\left(1-r_i\right)}^2}=2\sqrt[]{r_i}\mathrm{,}}\end{array}$ ugyanígy $\begin{array}{c}{\displaystyle E{E}_{i+1}=2\sqrt[]{r_{i+1}}\mathrm{,}}\end{array}$ tehát $\begin{array}{c}{\displaystyle E_{i+1}{E}_i=O_{i+1}O\text{'}{\text{'}}_{i+1}=\sqrt[]{O_i{O}_{i+1}^2-O_{i}O\text{'}{\text{'}}_{i+1}^2}=\sqrt[]{{\left(r_i+r_{i+1}\right)}^2-{\left(r_i-r_{i+1}\right)}^2}=2\sqrt[]{r_i{r}_{i+1}}\mathrm{.}}\end{array}$ Ezekkel $E{E}_i=E{E}_{i+1}+E_{i+1}{E}_i$-ből $\begin{array}{c}{\displaystyle 2\sqrt[]{r_i}=2\sqrt[]{r_{i+1}}+2\sqrt[]{r_i{r}_{i+1}}\mathrm{,}}\end{array}$ és a jobb oldal második tagjával osztva $\begin{array}{c}{\displaystyle \frac{1}{\sqrt[]{r_{i+1}}}=\frac{1}{\sqrt[]{r_i}}+1.}\end{array}$ (3) Innen $r_2=1/4$-del $r_3=1/9$, és ebből $r_4=1/16$. Az így adódott $\begin{array}{c}{\displaystyle r_i=\frac{1}{i^2}\mathrm{,}\frac{1}{\sqrt[]{r_i}}=i}\end{array}$ (4) sejtés teljes indukcióval azonnal igazolható; ha ugyanis (4) érvényes, akkor (3)-ból $\begin{array}{c}{\displaystyle \frac{1}{\sqrt[]{r_{i+1}}}=i+\mathrm{1,}\text{tehát}{r}_{i+1}=\frac{1}{{\left(i+1\right)}^2}\mathrm{.}}\end{array}$ Ezzel a feladat kérdésére a választ megkaptuk.