Feladat:	1961. évi Matematika OKTV II. forduló 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1962/január, 2 - 3. oldal		PDF  |  MathML
Témakör(ök):	Húrnégyszögek, Középponti és kerületi szögek, Háromszögek hasonlósága, Kör (és részhalmaza), mint mértani hely, OKTV
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Matematika OKTV II. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.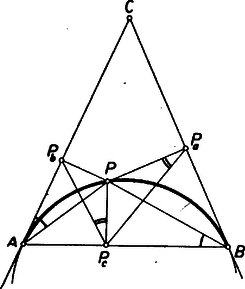   Megmutatjuk, hogy a feladat követelményeit kielégítő minden pontból ugyanakkora szög alatt látszik az $AB$ alap. Legyen az $ABC$ háromszögben $CA=CB$, és $P$ egy a feltételnek megfelelő pont, azaz ha vetülete az $AB$ alapra $P_c$, és a $CA$, $CB$ szárra $P_b$, $P_a$, akkor $\begin{array}{c}{\displaystyle P{P}_a\cdot P{P}_b=P{P}_c^2\mathrm{.}}\end{array}$ $P{P}_{a}B{P}_c$ és $P{P}_{c}A{P}_b$ a $PB$, ill. $PA$ átmérő fölötti Thalész-körbe írt húrnégyszögek. Ezért ${\displaystyle \begin{array}{c}\hfill {\displaystyle P_{a}P{P}_c\sphericalangle ={180}^{\circ }-P_{a}B{P}_c\sphericalangle ={180}^{\circ }-CBA\sphericalangle ={180}^{\circ }-CAB\sphericalangle =}\hfill \\ \hfill {\displaystyle ={180}^{\circ }-P_{b}A{P}_c\sphericalangle =P_{c}P{P}_b\sphericalangle \mathrm{.}}\hfill \end{array}}$ Másrészt a feltevésből átalakítással $\begin{array}{c}{\displaystyle P{P}_a:P{P}_c=P{P}_c:P{P}_b\mathrm{.}}\end{array}$ Ezek szerint a $P_{a}P{P}_c$ és $P_{c}P{P}_b$ háromszögek hasonlók, tehát $P_c{P}_{a}P\sphericalangle =P_b{P}_{c}P\sphericalangle$. Ebből ismét az említett húrnégyszögekre tekintettel $P_{c}BP\sphericalangle =P_{b}AP\sphericalangle$, vagyis $ABP\sphericalangle =CAP\sphericalangle$. Így az $ABP$ háromszögben $\begin{array}{c}{\displaystyle PAB\sphericalangle +ABP\sphericalangle =CAB\sphericalangle -CAP\sphericalangle +ABP\sphericalangle =CAB\sphericalangle \mathrm{,}}\end{array}$ tehát $APB\sphericalangle ={180}^{\circ }-CAB\sphericalangle$, állandó. Eszerint $P$ az $AB$ szakasz $\omega ={180}^{\circ }-CAB\sphericalangle$ nyílású látószög-körívének pontja. Csak arról az $i$ körívről lehet szó, amely $AB$-nek $C$-vel megegyező oldalán van, mert $P$-nek az $ABC$ háromszög belsejében kell lennie. Mivel $CAB\sphericalangle <{90}^{\circ }$, azért $\omega >{90}^{\circ }$; így $i$-nek $O$ középpontja $AB$-nek $C$-vel ellentétes oldalán van, és az $i$-hez tartozó középponti szög $AOB\sphericalangle ={360}^{\circ }-2\omega =2CAB\sphericalangle$. Ezért az $ABO$ háromszögből $BAO\sphericalangle =ABO\sphericalangle ={90}^{\circ }-CAB\sphericalangle$, tehát $OA\perp CA$. Eszerint az $AC$, $BC$ szár $A$, ill. $B$-ben érinti $i$-t, vagyis $A$ és $B$-t nem tekintve $i$ minden pontja az $ABC$ háromszög belsejében van. Megmutatjuk, hogy $i$ minden $Q$ pontja megfelel a követelménynek. Legyen $Q$ vetülete az $AB$, $AC$, $BC$ oldalon $Q_c$, $Q_b$, $Q_a$. Mivel $Q$ az $i$ íven van, $AQB\sphericalangle ={180}^{\circ }-CAB\sphericalangle$. Így az $ABQ$ háromszögből $\begin{array}{c}{\displaystyle QBA\sphericalangle ={180}^{\circ }-AQB\sphericalangle -QAB\sphericalangle =CAB\sphericalangle -QAB\sphericalangle =CAQ\sphericalangle \mathrm{,}}\end{array}$ másrészt $Q{Q}_{a}B{Q}_c$ és $Q{Q}_{c}A{Q}_b$ húrnégyszögek, ezért $\begin{array}{c}{\displaystyle Q{Q}_a{Q}_c\sphericalangle =QB{Q}_c\sphericalangle =QBA\sphericalangle =CAQ\sphericalangle =Q_{b}AQ\sphericalangle =Q_b{Q}_{c}Q\sphericalangle \mathrm{,}}\end{array}$ és ugyanígy $QBC\sphericalangle =QAB\sphericalangle$-ből $Q{Q}_c{Q}_a\sphericalangle =Q{Q}_b{Q}_c\sphericalangle$. Eszerint a $Q{Q}_a{Q}_c$ és $Q{Q}_c{Q}_b$ háromszögek hasonlók, ebből $Q{Q}_a:Q{Q}_c=Q{Q}_c:Q{Q}_b$ és $Q{Q}_a\cdot Q{Q}_b=Q{Q}_c^2$, amit bizonyítani akartunk. Ezek szerint az előírt tulajdonságú pontok mértani helye az adott egyenlő szárú háromszög szárait az alap végpontjaiban érintő körnek az érintési pontok közé eső kisebb íve, az érintési pontokat nem számítva.   Megjegyzések. 1. Több versenyző kimondta és bebizonyította, hogy az említett kör minden pontjára nézve a száraktól mért távolságok mértani közepe egyenlő az alaptól mért távolsággal. 2. Többen trigonometriai számításokon keresztül jutottak arra, hogy az $APB$ szög független a $P$ pont helyzetétől.