Kezdőlap


Feladat:	1961. évi Matematika OKTV I. forduló 2. feladata	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1961/október, 50. oldal		PDF \| MathML
Témakör(ök):	Középvonal, Háromszög-egyenlőtlenség alkalmazásai, OKTV
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Matematika OKTV I. forduló 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az $A B C D$ négyszög (2. ábra) $A D$ és $B C$ oldalának felezőpontja $E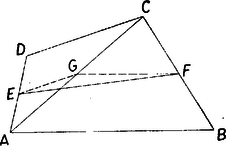$ és $F$ , és $E F = (A B + D C) / 2$ .

2. ábra

Azt fogjuk bebizonyítani, hogy

A B

és

C D

párhuzamosak. Jelöljük az

A C

átló felezőpontját

G

-vel. Ekkor egyrészt

E G

, mint az

A C D

háromszög középvonala, párhuzamos

D C

-vel és fele akkora; és hasonlóan az

A B C

háromszög

G F

középvonala párhuzamos

A B

-vel és fele akkora. Másrészt az

E F G

háromszögből ‐ ha ez valódi háromszög, tehát

G

nem esik az

E F

egyenesre ‐

\begin{matrix} E F < E G + G F = \frac{1}{2} (D C + A B) . \end{matrix}

Eszerint a bal oldal a jobbal egyenlő csak akkor lehet, ha

G

E F

egyenesen van. Ekkor

\begin{matrix} D C | | E F | | A B, \end{matrix}

vagyis az

A B C D

négyszög trapéz, és ezt kellett bizonyítani.

Megjegyzés. A feladat következő általánosítását tartalmazza Bollobás Béla dolgozata: Ha az

A B C D

négyszög

A D

és

B C

oldalát az

M

, illetőleg

N

pont

m : n

arányban osztja és

\begin{matrix} M N = \frac{m \cdot D C + n \cdot A B}{m + n}, \end{matrix}

(amit így szokás mondani:

M N

D C

és

A B

oldalnak

m

, illetőleg

n

súllyal súlyozott számtani közepe), akkor

A B

párhuzamos

C D

-vel, a négyszög trapéz. Az állítás az

A C

átlót

m : n

arányban osztó

P

pont segítségül vételével a fenti megoldáshoz hasonlóan bizonyítható.