Kezdőlap


Feladat:	1961. évi Matematika OKTV I. forduló 1. feladata	Korcsoport: 18-	Nehézségi fok: átlagos
Füzet:	1961/október, 49 - 50. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Pitagorasz-tétel alkalmazásai, Szögfüggvények, síkgeometriai számítások, Koszinusztétel alkalmazása, OKTV
Hivatkozás(ok):	Feladatok: 1961/szeptember: 1961. évi Matematika OKTV I. forduló 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a léggömb $L$ , merőleges vetülete a vízszintes talajon (talppontja) $T$ ; a megfigyelők $A$ és $B$ ; a léggömb emelkedési szöge az $A$ pontból $α = 45^{\circ}$ , a $B$ pontból $β = 22, 5^{\circ}$ , a két megfigyelő távolsága $A B = d = 1600 m$ , a $T A$ déli és $T B$ északnyugati irányok hajlásszöge 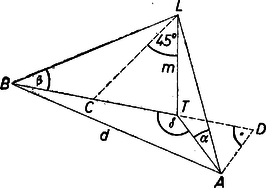$δ = 135^{\circ}$ (1. ábra).

1. ábra

‐ Az

A T L

derékszögű háromszög egyenlő szárú, mert

α = 45^{\circ}

, tehát

A T

egyenlő a keresett

T L

magassággal ‐ jelöljük ezt röviden

m

-mel. Húzzunk a

B T L

háromszög

L

csúcsából

L T

-vel

45^{\circ}

-ot bezáró egyenest. Mivel

B L T ∢ = 90^{\circ} - L B T ∢ = 67, 5 >

> 45^{\circ}

, azért egyenesünk a

B T

szakaszt metszi egy

C

pontban.

T C = T L = m

és

B L C ∢ = B L T ∢ - 45^{\circ} = 22, 5^{\circ} = T B L ∢ = C B L ∢

, vagyis a

B C L

háromszög egyenlő szárú:

B C = C L = m \sqrt[]{2}

.
Jelöljük az

A

pont merőleges vetületét a

B T

egyenesen

D

-vel. Ekkor az

A D T

derékszögű háromszög is egyenlő szárú, mert

T

-nél levő szöge

A T D ∢ = 180^{\circ} - A T B ∢ = 45^{\circ}

, s így

A D = D T = m / \sqrt[]{2}

.
Az

A B D

derékszögű háromszög átfogójának hossza adott:

d = 1600 m

, befogóit pedig sikerült kifejezni a keresett

m

magassággal:

A D = m / \sqrt[]{2}

B D = B C + C T + T D = m \sqrt[]{2} + m + m / \sqrt[]{2}

. Így Pythagorász tétele szerint

\begin{matrix} A D^{2} + D B^{2} = {(\frac{m}{\sqrt[]{2}})}^{2} + {(m \sqrt[]{2} + m + \frac{m}{\sqrt[]{2}})}^{2} = A B^{2} = 1600^{2} . \end{matrix}

Innen

\begin{matrix} m^{2} (\frac{1}{2} + 2 + 2 \sqrt[]{2} + 1 + 2 + \sqrt[]{2} + \frac{1}{2}) = m^{2} 3 \sqrt[]{2} (\sqrt[]{2} + 1) = 1600^{2}, \end{matrix}

vagyis

\begin{matrix} m = \frac{1600}{\sqrt[]{3 \sqrt[]{2} (\sqrt[]{2} + 1)}} = \frac{1600 \sqrt[]{\sqrt[]{2} - 1}}{\sqrt[]{3 \sqrt[]{2}}} = \frac{800}{3} \sqrt[]{\sqrt[]{8} (\sqrt[]{2} - 1) \cdot 3} = \frac{800}{3} \sqrt[]{12 - \sqrt[]{72}} \approx 500 m \end{matrix}

(méterre kerekítve).

II. megoldás. A feladatot általánosan, a talpponton átmenő vízszintes síkban tetszőleges helyzetű

A

és

B

megfigyelők és tetszőleges hegyes

α

és

β

emelkedési szögek esetére oldjuk meg.
Az

A T L

B T L

derékszögű háromszögből

A T = m ctg α

B T = m ctg β

, és így az

A T B

háromszögből a koszinusz-tétel alapján

\begin{matrix} d^{2} & = m^{2} {ctg}^{2} α + m^{2} {ctg}^{2} β - 2 m^{2} ctg α ctg β cos δ = \\ = m^{2} ({ctg}^{2} α + {ctg}^{2} β - 2 ctg α ctg β cos δ), \end{matrix}

és innen

\begin{matrix} m = \frac{d}{\sqrt[]{{ctg}^{2} α + {ctg}^{2} β - 2 ctg α ctg β cos δ}} . \end{matrix}

(Ha

A B T

valóságos háromszög, akkor a négyzetgyök alatt álló kifejezés pozitív, mert a koszinusz-tétel érvényes.)
A

d = 1600 m

α = 45^{\circ}

β = 22, 5^{\circ}

δ = 135^{\circ}

adatokkal

m \approx 500 m